Aufgabe:
Gemeinsame Dichtefunktion. Finden der marginalen Dichtefunktion und Verteilungsfunktion
Angenommen \( (X, Y)^{\prime} \) hat die Dichte
\( f(x, y)=\left\{\begin{array}{ll} \frac{x^{2}}{4} & \text { falls } 0 \leq x \leq 2 \text { und } 0 \leq x \leq y \leq 2 x \\ 0 & \text { sonst. } \end{array}\right. \)
(c) Bestimmen Sie die marginale Dichte und Verteilungsfunktion von \( Y \). Hinweis: Achten Sie auf die Skizze.
Problem/Ansatz:
fy(y) ist ja das Integral von f(x,y) über dx. Ich finde hier die Integralgrenzen für die marginale Dichte nicht.
Meine Idee war y/2 und y, weil x=y/2 und x=y. Das gibt aber 7*y^3/96. Wenn ich das nach dy über 0 bis y integriere ergibt das aber nicht die marginale Verteilungsfunktion, weil sie größer als 1 wird.
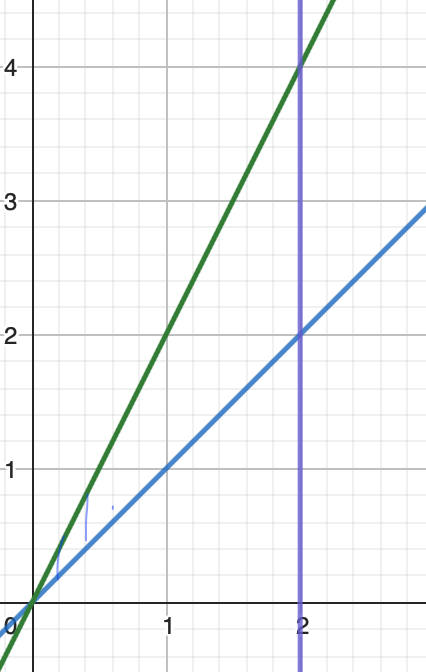
Skizze habe ich auch schon gemacht. Wie komme ich hier auf die Grenzen?