Wasserzuflussrate eines Wasserturms

Question

Kann mir jemand vielleicht den Ansatz für die untere Aufgabe b und d geben.

b) Ich bin auf die Idee gekommen den Integral von 0 bis 11 zu bilden und von 11 bis 24. Dies dann wiederum voneinander abziehen.

Comments

Zufallsrate eines Wasserturms

Es geht hier nicht um eine Zufallsrate eines Wasserturms.

---

Hab mich verschrieben. Ich meinte Wasserzuflussrate

Answer 1

zu f): Der Wasserinhalt des Wasserbehälters ist größer geworden, weil die Bilanzfläche innerhalb von vierundzwanzig Stunden offensichtlich positiv ist.

Answer 2

Ich bin auf die Idee gekommen den Integral von 0 bis 11 zu bilden und von 11 bis 24. Dies dann wiederum voneinander abziehen.

Du solltest nur die Frage genau lesen. Du sollst nichts berechnen, sondern nur abschätzen. Schätze als die Flächen oberhalb und unterhalb der x-Achse im Bereich von 0 bis 24 ab und bilde die Differenz aus der Summe der Flächen oberhalb der x-Achse und der Fläche unterhalb der x-Achse. Du solltest näherungsweise auf 2880 m³ kommen die du natürlich auch ausrechnen könntest. Aber wie gesagt: Ausrechnen ist hier nicht gefordert.

Comments

wie kann ich dies denn abschätzen ohne zu rechnen?

---

Um das zu tun müsste man auch erstmal die Nullstellen bestimmen.

Oder man findet einen kürzeren Weg.

---

Um das zu tun müsste man auch erstmal die Nullstellen bestimmen. Oder man findet einen kürzeren Weg.

Genau. Nicht die Flächen bestimmen, sondern gleich das Integral bilden.

Nullstellen wurden auch unter b) berechnen und das Integral ist noch uim 2. Teil unter b) zu berechnen.

---

also gilt für b: \( \int\limits_{0}^{21.0670333} f(t)  d x \)

---

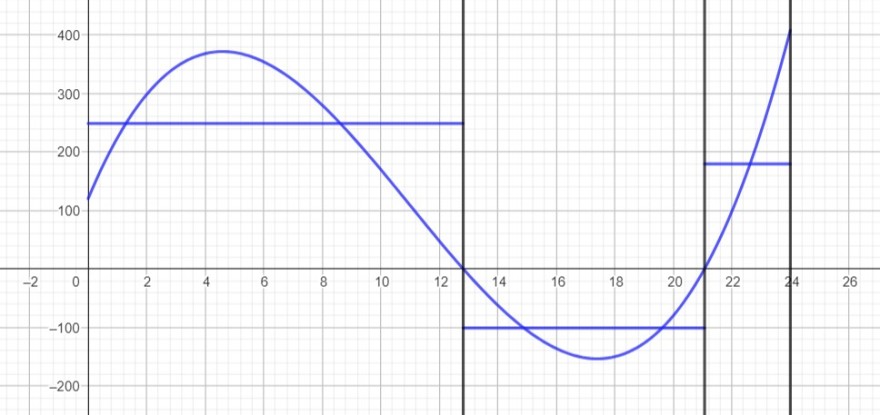
wie kann ich dies denn abschätzen ohne zu rechnen?

Ich zeichne mir dazu die mittleren Zufluss- und Abflussraten in den Intervallen ein.

Das ist eine horizontale Gerade, welche mit der x-Achse eine genauso große Fäche bildet wie der Graph in dem Intervall.

---

Man kann sich gut vorstellen das man ober bzw. unterhalb der x-Achse ein Teil einer Wasserwelle hat. Dann versucht man sich vorzustellen wie hoch das Wasser dann wohl steht, wenn man diesen Teil der Welle zur ruhe kommen lässt.

---

also gilt für b

Nimm das Integral von 0 bis 24. Dann passt das.