Aufgabe:
Ich habe folgende Aufgabe und die dazugehörige Lösung.
Soweit versteh ich aller außer den rot markierten Bereich.
Was hat das mit dem tangens zu tun und wie kommt man auf Jy=Jx•0,5 bzw. Jx=2•Jy ?
Problem/Ansatz:
Text erkannt:
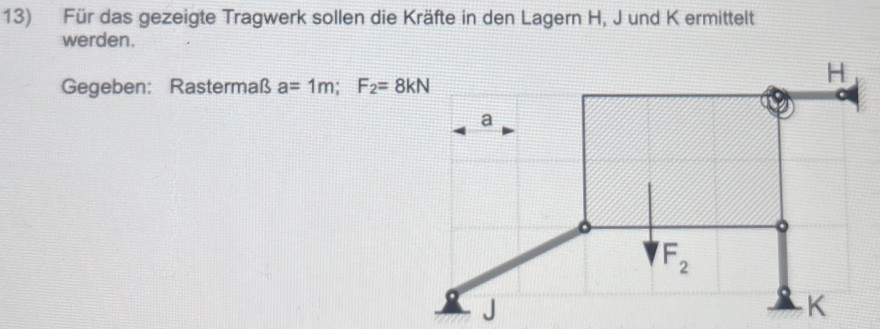
13) Für das gezeigte Tragwerk sollen die Kräfte in den Lagern \( \mathrm{H}, \mathrm{J} \) und K ermittelt werden.
Gegeben: Rastermaß \( a=1 \mathrm{~m} ; \quad F_{2}=8 \mathrm{kN} \)

Text erkannt:
13) \( \quad H=32 \mathrm{kN}(\rightarrow) ; \quad K=24 \mathrm{kN}(\uparrow) ; \quad J=35,82 \mathrm{kN} ; \quad \alpha_{J}=26,57^{\circ} \) (zur neg. \( x \)-Achse) frei:
(1) \( \Sigma F_{x} \stackrel{!}{=} 0: J_{x}+H \) \( =0 \)
(2) \( \sum F_{y} \stackrel{1}{=} 0: J_{y}-F_{z}+K \) \( =0 \)
(3) \( \sum M_{(J)} \stackrel{1}{=} 0:-F_{2} \cdot 1 m+K \cdot 3 m-H \cdot 2 m=0 \)
oder
\( \text { (4) } \sum M_{(k)} \stackrel{1}{=}=0: F_{2} \cdot 2 m-J_{y} \cdot 3 m-H \cdot 2 m=0 \)
oder
(S) \( \Sigma M_{(H)} \stackrel{!}{=} 0: F_{2} \cdot 2 \mu h+J_{x} \cdot 2 \mu h-J_{y} \cdot 3 \mu h=0 \) optimal ist (5); wg. \( \tan \alpha_{j}=\frac{1}{2}=\frac{J_{y}}{J_{x}} \) folgt:
(6)
\( J_{y}=J_{x} \cdot 0,5 \text { biw. } J_{x}=2 \cdot J_{y} \)
aus (5) folgt: \( 2 F_{2}+2 J_{x}-0,5 \cdot 3 J_{x}=0 \)
\( 2 F_{2}+0,5 J x=0 \)
darans folgt : \( J_{x}=-4 f_{2}=-32 \mathrm{kN}(\sqcup \)
Aus (1) folgt : \( H=-J_{x}=+32 k \mathrm{~N}(\rightarrow \)
Aus (2) folgt: \( K=F-J y \)
Aus(6) folgt: \( J_{y}=0,5 J_{x}=-16 \mathrm{eN}(t) \)
so forgt \( \quad K=F_{2}+16 k N=24 k N(t) \)
zusammengefaßt: \( J=\sqrt{J_{x}^{2}+J_{y}^{2}}=\sqrt{1280} \) \( J=35,777 \mathrm{kN}(\boldsymbol{A}) 206,5^{\circ} \)
zur Woogrediten: \( \alpha_{j}=\arctan \frac{J_{y}}{J_{x}}=26,565^{\circ} \)
absolut : \( \alpha_{J}=206,565^{\circ} \)