Aufgabe:
Betrachten Sie die Funktion
Problem/Ansatz:
Ich bin mir unsicher was ich falsch gemacht habe...
Ich habe grundsätzlich beim ersten alle x werde in die Passenden Funktionen eingesetzt.
Unten habe ich die Inverse gebildet und dass selbe gemacht jedoch wird mir gesagt es fehlen werte bei 2!
Hat einer von euch eine Idee was ich Falsch gemacgt habe?
MFG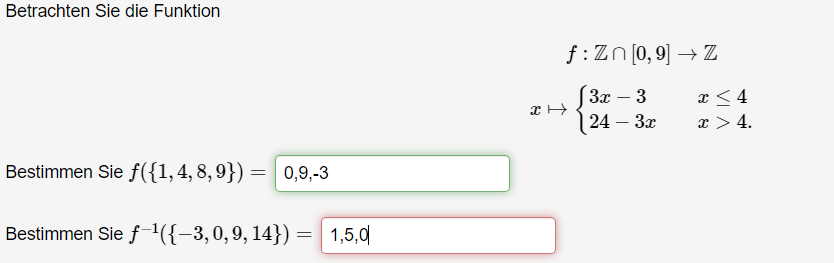
Text erkannt:
Betrachten Sie die Funktion
\( \begin{array}{c} f: \mathbb{Z} \cap[0,9] \rightarrow \mathbb{Z} \\ x \mapsto\left\{\begin{array}{ll} 3 x-3 & x \leq 4 \\ 24-3 x & x>4 \end{array}\right. \end{array} \)
Bestimmen Sie \( f(\{1,4,8,9\})=0,9,-3 \)
Bestimmen Sie \( f^{-1}(\{-3,0,9,14\})=1,5,0 \)