Aufgabe
(a) Gegeben sei eine Gerade \( g \in \mathbb{G} \), ein Punkt \( P \in \mathbb{P} \backslash g \) und sein Spiegelpunkt \( Q:=S_{g}(P) \). Zeigen Sie: Für alle \( A \in g \) ist auch \( S_{P Q}(A) \in g \).
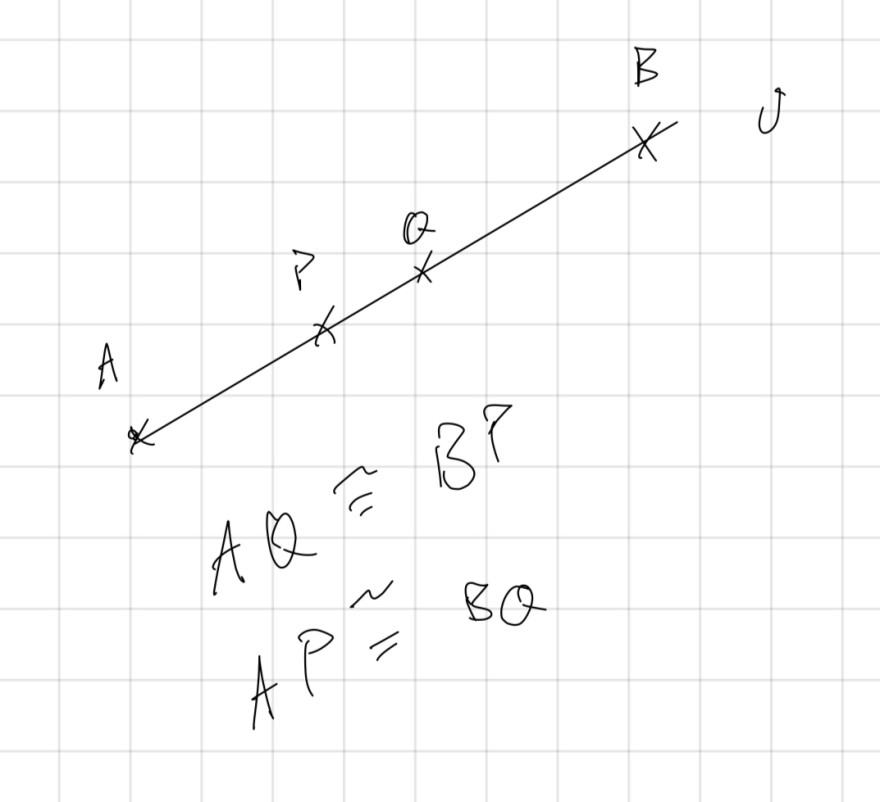
Hinweis: Zeigen Sie, dass die vier Strecken \( [A P],[A Q],[B P],[B Q]\left(\right. \) mit \( \left.B:=S_{P Q}(A)\right) \) alle kongruent zueinander sind.
Ist meine grobe Konstruktion der Aufgabe sinnvoll/richtig falls ja würde ich meinen Ansatz weiter verfolgen falls nein bräuchte ich nochmal einen Tipp bzw. die richtige Konstruktion der Aufgabe um sie zu verstehen