Aufgabe:
Geben Sie jeweils eine Parametrisierung der Mantelfläche des Rotationskörpers um die x3-Achse an und berechnen Sie den Flächeninhalt der Mantelfläche.
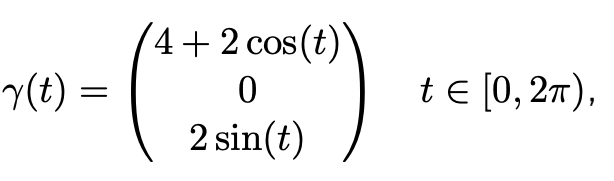
Text erkannt:
\( \gamma(t)=\left(\begin{array}{c}4+2 \cos (t) \\ 0 \\ 2 \sin (t)\end{array}\right) \quad t \in[0,2 \pi) \)
Moin, ich sitze gerade an der Aufgabe und komme leider nicht weiter. Wie berechne ich diese Aufgabe?