Wenn Funktion 2-Fach differenzierbar ist, ist diese auch n-fach wobei n>2 differenzierbar?

Question

Die Frage ist: wenn eine Funktion 2-Fach differenzierbar ist, ist dies auch n-fach wobei n>2 differenzierbar?
Wie ich es verstehe heißt es also, wenn sich eine Funktion 2 mal ableiten lässt, lässt sie sich auch n mal ableiten. Wobei die Lösung nicht unendlich sein darf wenn man etwas für x einsetzt. Korrekt? Ich finde aber kein Beispiel wo eine Funktion sich 2 mal ableiten lässt aber nicht beim 3. mal.
z.B. f(x) = x^2, f'(x) = 2x, f''(x) = 1, f'''(x)= 0 nun bleibt die Funktion immer null, der Grenzwert ist also immer 0 und somit differenzierbar. Ich würde also sagen eine 2-Fach differenzierbare Funktion ist n-Fach differenzierbar. Wie beweise ich es aber mit der Definition der Differenzierbarkeit?

Lg

Answer 1

Betrachte f(x)= x^3 für x≥0 und f(x)=x^4 für x<0.

An der Stelle 0 ist f 2-mal differenzierbar, aber nicht 3-mal.

Comments

f(x)= x^3 für x≥0 immer positiv
und f(x)=x^4 für x<0 ist immer positiv

f(x) = x^3

f'(x) = 3x
f''(x) = 3
f'''(x) = 0

bedeutet 0 das die Funktion nicht differenzierbar ist?

---

tut mir leid, ich habe folgendes nun raus:

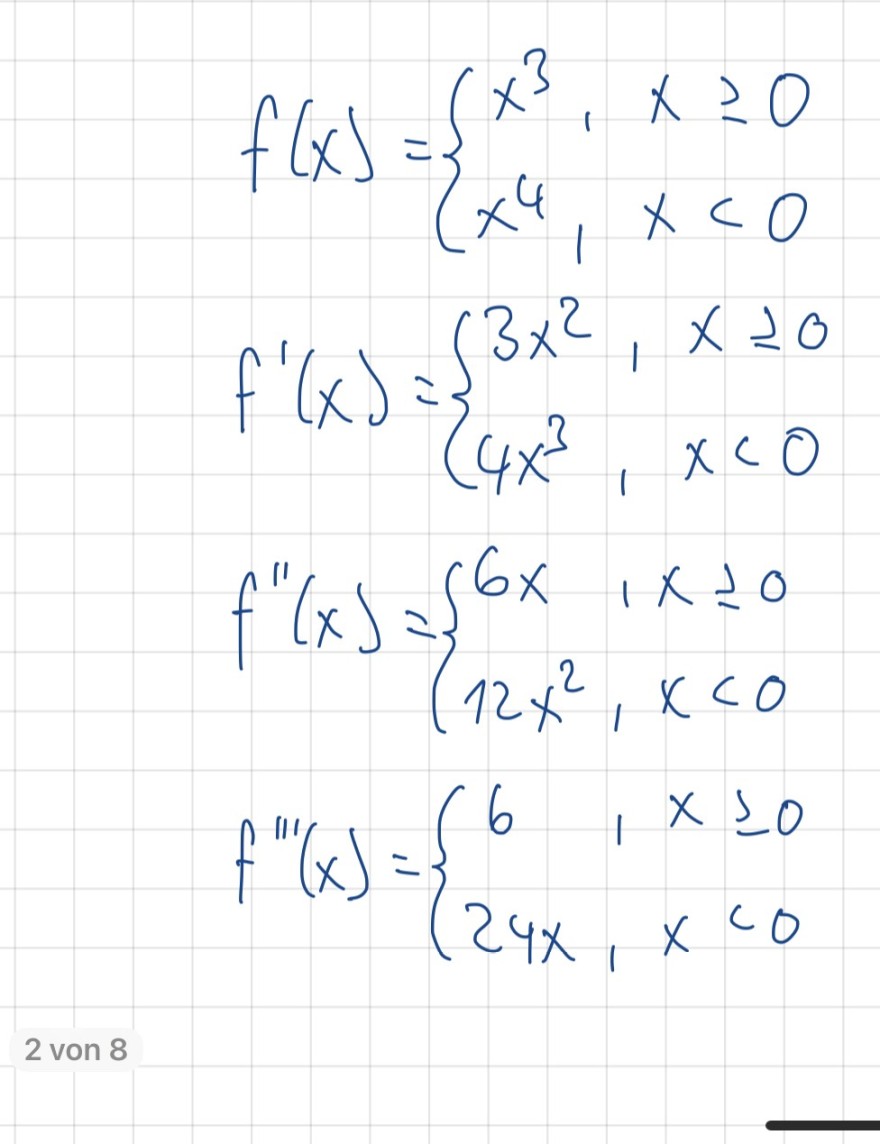
Text erkannt:

\( \begin{array}{l} f(x)=\left\{\begin{array}{ll} x^{3}, & x \geq 0 \\ x^{4}, & x<0 \end{array}\right. \\ f^{\prime}(x)=\left\{\begin{array}{ll} 3 x^{2}, & x \geq 0 \\ 4 x^{3}, & x<0 \end{array}\right. \\ f^{\prime \prime}(x)=\left\{\begin{array}{ll} 6 x, & x \geq 0 \\ 12 x^{2}, & x<0 \end{array}\right. \\ f^{\prime \prime \prime}(x)=\left\{\begin{array}{ll} 6, & x \geq 0 \\ 24 x, & x<0 \end{array}\right. \end{array} \)
2 von 8

Warum ist f'''(x) nun nicht differenzierbar?

---

Weil bei x=0 die rechtsseitige Ableitung 6 und die linksseitige 0 ist.

Wäre es diffb. müssten beide gleich sein.