Aufgabe:
Kann mir jemand bei den Aufgaben helfen und alle Aufgaben erklären. Die 1 hab ich schon gemacht. Ich bitte euch
Problem/Ansatz:
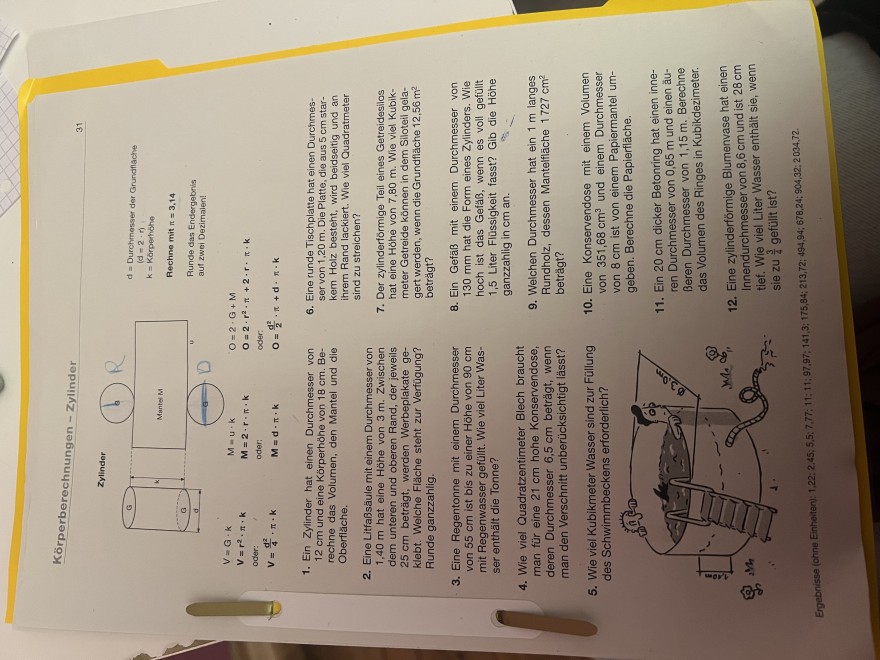
Text erkannt:
Körperberechnungen - Zylinder
31
\( \begin{aligned} d= & \text { Durchmesser der Grundilache } \\ & (d=2 \cdot r) \\ k & =\text { Körperhohe } \end{aligned} \)
Pechne mit \( \pi=3,14 \)
Runde das Endergebnis aut zwoi Dezimalen!
\( \begin{array}{l} V=G \cdot k \\ V=r^{2} \cdot \pi \cdot k \end{array} \)
\( M=u \cdot k \)
\( M=2 \cdot r \cdot \pi \cdot k \)
oder:
\( V=\frac{d^{2}}{4} \cdot \pi \cdot k \)
\( \begin{array}{l} O=2 \cdot G+M \\ O=2 \cdot r^{2} \cdot \pi+2 \cdot r \cdot \pi \cdot k \end{array} \)
oder:
oder:
\( M=d \cdot \pi \cdot k \)
\( 0=\frac{d^{2}}{2} \cdot \pi+d \cdot \pi \cdot k \)
6. Eine runde Tischplatte hat einen Durchmesser von \( 1,20 \mathrm{~m} \). Die Platte, die aus \( 5 \mathrm{~cm} \) starkem Holz besteht, wird beidseitig und an ihrem Rand lackiert. Wie viel Quadratmeter sind zu streichen?
2. Eine Litfaßsäule mit einem Durchmesser von \( 1,40 \mathrm{~m} \) hat eine Höhe von \( 3 \mathrm{~m} \). Zwischen dem unteren und oberen Rand, der jeweils \( 25 \mathrm{~cm} \) beträgt, werden Werbeplakate geklebt. Welche Fläche steht zur Verfügung? Runde ganzzahlig.
3. Eine Regentonne mit einem Durchmesser von \( 55 \mathrm{~cm} \) ist bis zu einer Höhe von \( 90 \mathrm{~cm} \) mit Regenwasser gefüllt. Wie viel Liter Wasser enthält die Tonne?
4. Wie viel Quadratzentimeter Blech braucht man für eine \( 21 \mathrm{~cm} \) hohe Konservendose, deren Durchmesser \( 6,5 \mathrm{~cm} \) beträgt, wenn man den Verschnitt unberücksichtigt lässt?
5. Wie viel Kubikmeter Wasser sind zur Füllung des Schwimmbeckens erforderlich?
7. Der zylinderförmige Teil eines Getreidesilos hat eine Höhe von \( 7,80 \mathrm{~m} \). Wie viel Kubikmeter Getreide können in dem Silotell gelagert werden, wenn die Grundfläche 12,56 \( \mathrm{m}^{2} \) beträgt?
1. Ein Zylinder hat einen Durchmesser von \( 12 \mathrm{~cm} \) und eine Körperhöhe von \( 18 \mathrm{~cm} \). Berechne das Volumen, den Mantel und die Oberfläche. beträgt?
8. Ein Gefäß mit einem Durchmesser von \( 130 \mathrm{~mm} \) hat die Form eines Zylinders. Wie hoch ist das Gefäß, wenn es voll gefüllt 1,5 Liter Flüssigkeit fasst? Gib die Höhe ganzzahlig in \( \mathrm{cm} \) an.
9. Welchen Durchmesser hat ein \( 1 \mathrm{~m} \) langes Rundholz, dessen Mantelfläche \( 1727 \mathrm{~cm}^{2} \) beträgt?
10. Eine Konservendose mit einem Volumen von \( 351,68 \mathrm{~cm}^{3} \) und einem Durchmesser von \( 8 \mathrm{~cm} \) ist von einem Papiermantel umgeben. Berechne die Papierfläche.
11. Ein \( 20 \mathrm{~cm} \) dicker Betonring hat einen inneren Durchmesser von \( 0,65 \mathrm{~m} \) und einen äuBeren Durchmesser von \( 1,15 \mathrm{~m} \). Berechne das Volumen des Ringes in Kubikdezimeter.
12. Eine zylinderförmige Blumenvase hat einen Innendurchmesser von \( 8,6 \mathrm{~cm} \) und ist \( 28 \mathrm{~cm} \) tief. Wie viel Liter Wasser enthält sie, wenn sie zu \( \frac{3}{4} \) gefüllt ist?
Ergebnisse (ohne Einheiten): 1,\( 22 ; 2,45 ; 5,5 ; 7,77 ; 11 ; 11 ; 97,97 ; 141,3 ; 175,84 ; 213,72 ; 494,94 ; 678,24 ; 904,32 ; 2034,72 \).