Den Strahlensatz mit mehren Schritten beweisen

Question

Aufgabe:

Text erkannt:

Seien \( G, H \subset \mathbb{R}^{2} \) Geraden mit \( G \cap H=\{p\}, a, a^{\prime} \in G \backslash\{p\} \) und \( b, b^{\prime} \in H \backslash\{p\} \). Weiter gelte \( G_{a, b-a} \| G_{a^{\prime}, b^{\prime}-a^{\prime}} \).

Wir wollen den Strahlensatz in mehreren Schritten beweisen, zeigen Sie dazu:
a) Es gibt \( \alpha, \beta, \mu \in \mathbb{R} \), sodass gilt:
\( a^{\prime}-p=\alpha \cdot(a-p) \quad b^{\prime}-p=\beta \cdot(b-p) \quad b^{\prime}-a^{\prime}=\mu \cdot(b-a) \)

Text erkannt:

Folgern Sie:
\( \frac{\left\|a^{\prime}-p\right\|}{\|a-p\|}=\frac{\left\|b^{\prime}-p\right\|}{\|b-p\|}=\frac{\left\|b^{\prime}-a^{\prime}\right\|}{\|b-a\|} \)

Problem/Ansatz:

Ich weiß leider gar nicht was ich machen soll

Answer 1

Zunächst werden Bezeichnungen korrigiert und eine Festlegung vorgenommen,

\( \vec{a} \) ist der Vektor, der zu A führt,

\( \vec{b} \) ist der Vektor, der zu B führt,

\( \vec{a'} \) ist der Vektor, der zu A' führt,

\( \vec{b'} \) ist der Vektor, der zu B' führt,

\( \vec{p} \) ist der Vektor, der zu P führt:

Wenn jetzt noch Fragen sind, bitte nachfragen.

Comments

Ich weiß aber nicht wie ich das nutzen kann mit den Definitionen/Sätzen/Lemmas die wir nur kennen und nutzen dürfen

Text erkannt:

Lemma 3.125 Seien \( p, q \in \mathbb{R}^{2} \) und \( v, w \in \mathbb{R}^{2} \backslash\{\mathbf{0}\} \), dann gilt:
a) \( q \in G_{p, v} \quad \Leftrightarrow \quad G_{p, v}=G_{q, \nu} \quad \Leftrightarrow \quad p \in G_{q, \nu} \).
b) \( G_{p, \nu}=G_{p, w} \quad \Leftrightarrow \quad(\nu, w) \) ist linear abhängig.

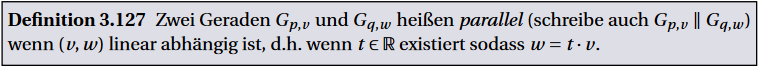
Text erkannt:

Definition 3.127 Zwei Geraden \( G_{p, v} \) und \( G_{q, w} \) heißen parallel (schreibe auch \( G_{p, v} \| G_{q, w} \) ) wenn \( (\nu, w) \) linear abhängig ist, d.h. wenn \( t \in \mathbb{R} \) existiert sodass \( w=t \cdot \nu \).

Text erkannt:

Satz 3.129 Zwei Geraden \( G, G^{\prime} \) sind genau dann parallel, wenn sie gleich sind \( \left(G=G^{\prime}\right) \) oder sich nicht schneiden \( \left(G \cap G^{\prime}=\varnothing\right) \).

---

Wobei ich raus gefunden habe das die c Aufgabe die Strahlensätze wieder geben oder?