Text erkannt:
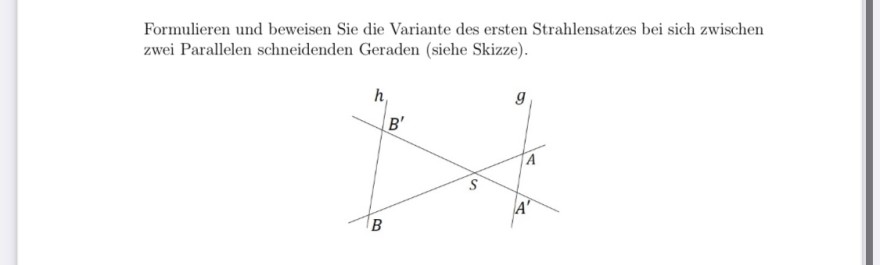
Formulieren und beweisen Sie die Variante des ersten Strahlensatzes bei sich zwischen zwei Parallelen schneidenden Geraden (siehe Skizze).
Text erkannt:
Aufgabe 2 (5 Punkte)
Formulieren und beweisen Sie die Variante des ersten Strahlensatzes bei sich zwischen zwei Parallelen schneidenden Geraden (siehe Skizze).
Text erkannt:
Aufgabe 1 (6 Punkte)
a) Lösen Sie folgende Schulbuchaufgabe und begründen Sie Ihr Vorgehen.
Die Zeichnung zeigt, wie man mithilfe von Fluchtstäben bei den Punkten \( \mathrm{A}, \mathrm{B} \), \( \mathrm{C} \) und \( \mathrm{D} \) die Breite cines Flusses bestimmen kann, indem man einen Punkt P am gegenüberliegenden Ufer anpeilt. \( \mathrm{Um} \mathrm{BC} \| \mathrm{AD} \) zu erreichen, visiert man von \( \mathrm{A} \) über \( \mathrm{D} \) und von \( \mathrm{B} \) über \( \mathrm{C} \) einen sehr weit entfernten Punkt im Gelände an. Die Entfernungen a, b, d bestimmt man durch Abschreiten \( (1 \) Schritt \( \approx 1 \mathrm{~m} \) ). Beispiel: \( \mathrm{a}=\mathrm{d}=20 \mathrm{~m}, \mathrm{~b}=28 \mathrm{~m} \). Berechne \( \mathrm{x} \).
b) In der folgenden Skizze gelte \( g \| h \) und \( \frac{u}{v}=\frac{1}{2} \).
Berechnen Sie \( \frac{x}{y} \) und begründen Sie Ihr Vorgehen.