Aufgabe:
Bei Ableitung der 2 Funktion habe ich irgendwo ein Fehler den ich nicht sehe.
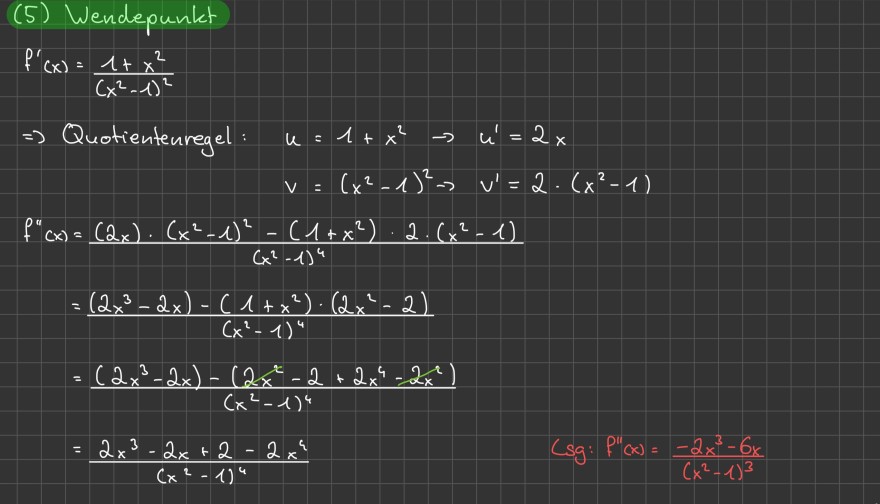
Text erkannt:
(5) Wendepunkt
\( f^{\prime}(x)=\frac{1+x^{2}}{\left(x^{2}-1\right)^{2}} \)
\( \Rightarrow \) Quotientenregel: \( u=1+x^{2} \rightarrow u^{\prime}=2 x \)
\( v=\left(x^{2}-1\right)^{2} \rightarrow v^{\prime}=2 \cdot\left(x^{2}-1\right) \)
\( \begin{aligned} f^{\prime \prime}(x) & =\frac{(2 x) \cdot\left(x^{2}-1\right)^{2}-\left(1+x^{2}\right) \cdot 2 \cdot\left(x^{2}-1\right)}{\left(x^{2}-1\right)^{4}} \\ & =\frac{\left(2 x^{3}-2 x\right)-\left(1+x^{2}\right) \cdot\left(2 x^{2}-2\right)}{\left(x^{2}-1\right)^{4}} \\ & =\frac{\left(2 x^{3}-2 x\right)-\left(2 x^{x}-2+2 x^{4}-2 x^{2}\right)}{\left(x^{2}-1\right)^{4}} \quad \quad \text { (sg: } f^{\prime \prime}(x)=\frac{-2 x^{3}-6 x}{\left(x^{2}-1\right)^{3}} \\ & =\frac{2 x^{3}-2 x+2-2 x^{4}}{\left(x^{2}-1\right)^{4}} \end{aligned} \)