Aufgabe:
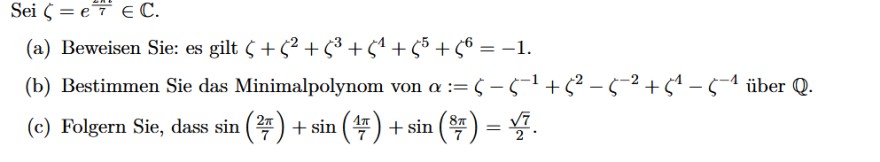
Text erkannt:
Sei \( \zeta=e^{-\frac{2\pi}{7}} \in \mathbb{C} \).
(a) Beweisen Sie: es gilt \( \zeta+\zeta^{2}+\zeta^{3}+\zeta^{4}+\zeta^{5}+\zeta^{6}=-1 \).
(b) Bestimmen Sie das Minimalpolynom von \( \alpha:=\zeta-\zeta^{-1}+\zeta^{2}-\zeta^{-2}+\zeta^{4}-\zeta^{-4} \) über \( \mathbb{Q} \).
(c) Folgern Sie, dass \( \sin \left(\frac{2 \pi}{7}\right)+\sin \left(\frac{4 \pi}{7}\right)+\sin \left(\frac{8 \pi}{7}\right)=\frac{\sqrt{7}}{2} \).
Problem/Ansatz:
Die a habe ich.
Bei der b habe ich Euler verwendet aber ich komme nicht weiter. Ich habe da stehen
-a^2*0,25= der Term in c. Aber das bekomme ich nur mit dem Internet berechnet. Ich vermute ich muss Aufgabenteil a einsetzen, aber ich weiß nicht wie.