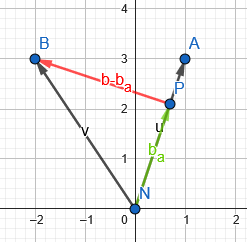
Aloha :)
Wenn du diese Aufgabe verstehst, hast du ganz viel über Vektorrechnung verstanden.
Daher versuche ich mal eine ausführliche Erklärung.
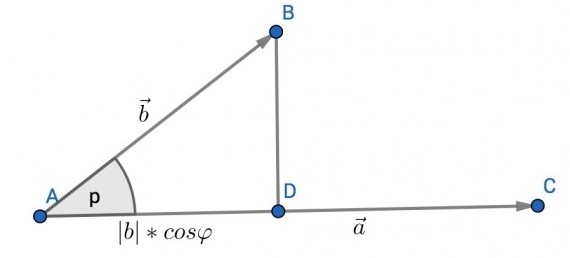
Der Vektor \(\vec b\) in dem Bild entspricht dem Vektor \(\overrightarrow{AB}\). Um von \(A\) nach \(B\) zu gelangen, könntest du auch zuerst den Vektor \(\overrightarrow{AD}\) entlang gehen und danach den Vektor \(\overrightarrow{DB}\) entlang. Der Vektor \(\vec b_\parallel\coloneqq\overrightarrow{AD}\) ist die Komponente von \(\vec b\), die parallel zum Vektor \(\vec a\) verläuft. Und die Komponente \(\vec b_\perp\coloneqq\overrightarrow{DB}\) ist die Komponente von \(\vec b\), die senkrecht auf dem Vektor \(\vec a\) steht:$$\underbrace{\overrightarrow{AB}}_{\small \vec b}=\underbrace{\overrightarrow{AD}}_{\small\vec b_\parallel}+\underbrace{\overrightarrow{DB}}_{\small \vec b_\perp}$$
Die zu \(\vec a\) parallele Komponene \(\vec b_\parallel\) nennt man auch "die Projektion von \(\vec b\) auf \(\vec a\)" und schreibt statt der parallelen Striche den Vektor \(\vec a\) hin, auf den projeziert wird: \(\green{\vec b_{\vec a}=\vec b_\parallel}\)
Damit ist dann auch klar, was der Vektor \((\vec b-\vec b_{\vec a})\) ist. Wenn du vom Vektor \(\vec b=\overrightarrow{AB}\) den Vektor \(\vec b_a=\overrightarrow{AD}\) subtrahierst, bleibt der zu \(\vec a\) senkrechte Anteil \(\overrightarrow{BD}\) von \(\vec b\) übrig:$$\underbrace{\overrightarrow{AB}}_{\small\vec b}-\underbrace{\overrightarrow{AD}}_{\small\vec b_\parallel}=\underbrace{\overrightarrow{DB}}_{\small\vec b_\perp}\quad\Longleftrightarrow\quad\red{\vec b_\perp=}\vec b-\vec b_\parallel=\red{\vec b-\vec b_{\vec a}}$$
Berechnet wird die Projektion \(\vec b_{\vec a}\) durch 2-malige Multiplikation von \(\vec b\) mit dem normierten Einheitsvektor \(\vec a^0\) von \(\vec a\). Die Rechnung wäre also:$$\vec a^0=\frac{1}{\|\vec a\|}\,\vec a=\frac{1}{\sqrt{1^2+3^2}}\binom{1}{3}=\frac{1}{\sqrt{10}}\binom{1}{3}$$$$\green{\vec b_a}=\left(\vec b\cdot\vec a^0\right)\cdot\vec a^0=\left(\binom{-2}{3}\cdot\frac{1}{\sqrt{10}}\binom{1}{3}\right)\cdot\frac{1}{\sqrt{10}}\binom{1}{3}=\frac{7}{10}\binom{1}{3}=\green{\binom{0,7}{2,1}}$$$$\red{\vec b-\vec b_{\vec a}}=\binom{-2}{3}-\green{\binom{0,7}{2,1}}=\red{\binom{-2,7}{0,9}}$$
Du sollst aber nicht rechnen, sondern zeichnen und abschätzen (bzw. messen):