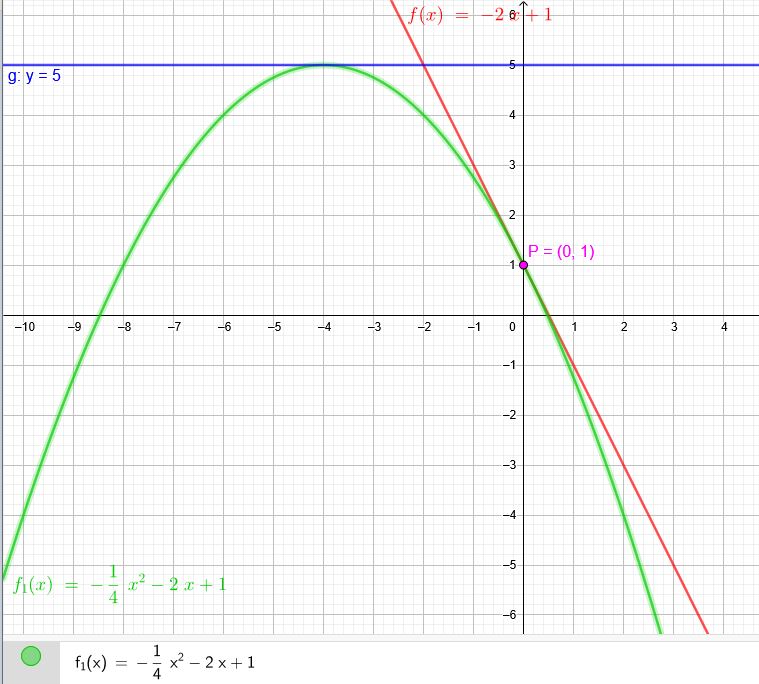
\(f(x)=ax^2+bx+c\)
\(P(0|1)\)
\(f(0)=c\)
1.)
\(c=1\)
\(f(x)=ax^2+bx+1\)
\(f'(x)=2ax+b\)
\(f'(0)=b\)
2.)
\(b=-2\)
\(f(x)=ax^2-2x+1\)
\(ax^2-2x+1=5\)
\(ax^2-2x=4 |:a\)
\(x^2-\frac{2}{a}x=\frac{4}{a}\)
\(x^2-\frac{2}{a}x+(\frac{1}{a})^2=\frac{4}{a}+(\frac{1}{a})^2=\frac{4a+1}{a^2}\)
\((x-\frac{1}{a})^2=\frac{4a+1}{a^2} |\pm\sqrt{~~}\)
1.)
\(x-\frac{1}{a}=\sqrt{\frac{4a+1}{a^2}}=\frac{1}{a}\sqrt{4a+1}\)
\(x_1=\frac{1}{a}+\frac{1}{a}\sqrt{4a+1}\)
2.)
\(x-\frac{1}{a}=-\frac{1}{a}\sqrt{4a+1}\)
\(x_2=\frac{1}{a}-\frac{1}{a}\sqrt{4a+1}\)
\(f(x)=ax^2-2x+1\)
\(f'(x)=2ax-2\)
1.)
\(f'(\frac{1}{a}+\frac{1}{a}\sqrt{4a+1})=2a \cdot (\frac{1}{a}+\frac{1}{a}\sqrt{4a+1})-2=2\sqrt{4a+1}\)
\(2\sqrt{4a+1}=0\)
\(a=-\frac{1}{4}\)
\(f_1(x)=-\frac{1}{4}x^2-2x+1\)
Nun noch für 2.)