Bestimmen Sie die Koordinaten des Punktes D(a b) im .Quadranten so, dass das Mittenviereck von ABCD ein Quadrat ist.

Question

Aufgabe:

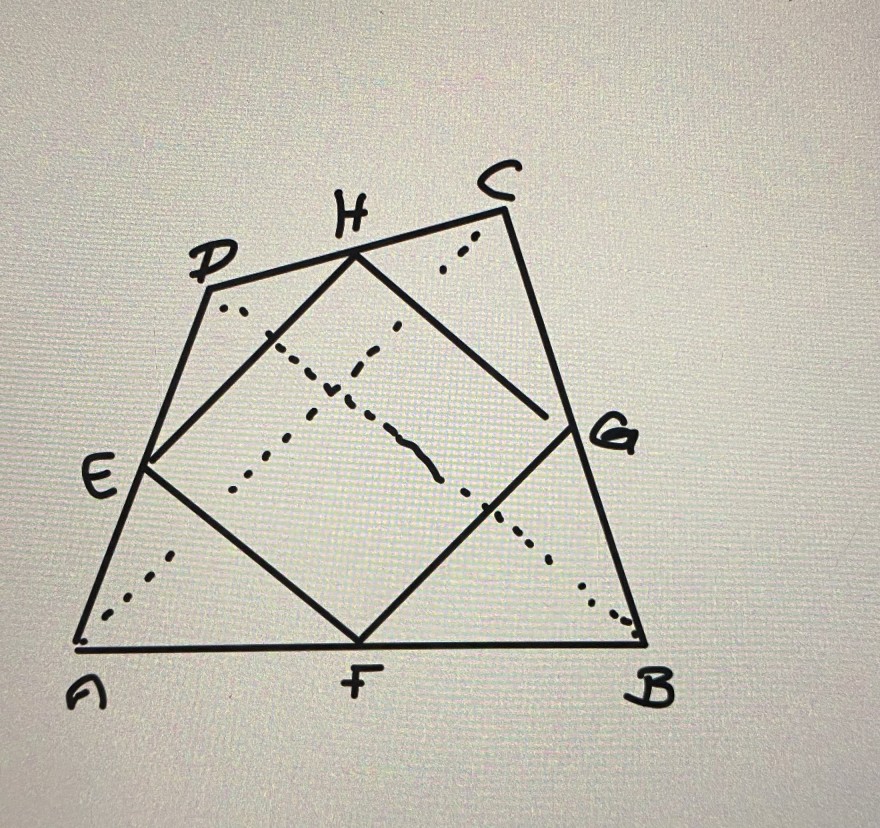
Verbindet man in einem beliebigen Viereck ABCD die Seitenmitten E,F,G und H, so erhält man ein Parallelogramm, denn nach den Strahlensätzen sind zum Beispiel die Seiten EF und GH parallel zur Diagonalen BD und halb so lang wie diese.

B) Gegeben sind die Punkte A(2/8), B(0|0) und C(4|2)
Bestimmen Sie die Koordinaten des Punktes D(a b) im .Quadranten so, dass das Mittenviereck von ABCD ein Quadrat ist.

Problem/Ansatz:

Ich verzweifle an dieser Aufgabe leider komplett… Kann mir bitte jemand helfen? Danke schön!

Comments

Wenn Du Dir eine Skizze gemacht hast, so sollte diese in etwa so aussehen:

an welcher Stelle kommst Du dabei nicht weiter?

PS.: Die Koordinaten von A, B und C sind etwas ungünstig gewählt. Kannst Du bitte nochmal prüfen, ob die Koordinaten in Deiner Frage mit denen in der Originalaufgabenstellung überein stimmen.

Answer 1

Mit den gegebenen Punkten A;B,C hast du ein Dreieck und darin seine Mittellinie FG. Sie ist halb so lang wie AC.

Die nächste Mittellinie GH ist so lang wie FG und halb so lang wie BD.

Also muss BD so lang sein wie AC, und BD muss senkrecht auf AC stehen (sonst gäbe es kein Quadrat).

Fälle also das Lot von B auf AC (bzw. berechne die Gleichung der Lotgeraden), und verlängere dieses Lot so weit über AC hinaus, dass du einen Punkt D erreichst mit \(\overline{AC}=\overline{BD}\).

Comments

Benutzt du Kristallkugel, Kaffeesatz oder was sonst ?

---

Wieso?

Die Aufgabe ist auch ohne Angabe des Quadranten, in dem der Punkt D liegen soll, lösbar.

Es gibt aber tatsächlich noch eine zweite Lösung, wenn das Viereck konkav ist und D bezüglich AC in der selben Halbebene liegt wie B.

Dann müsste das Viereck aber (bei üblicher Benennung entgegen dem Uhrzeigersinn) ADBC heißen.

---

wenn das Viereck konkav ist

Du meinst wohl "überschlagen", denn deines ist tatsächlich konkav.

Dann müsste das Viereck aber (bei üblicher Benennung entgegen dem Uhrzeigersinn) ADBC heißen

und dann wäre es wiederum konvex.