Text erkannt:
Aufgabe 3
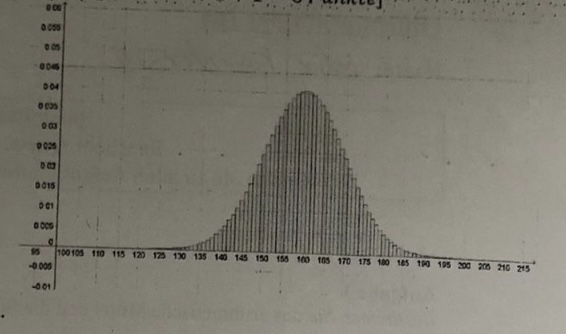
Das nebenstehende Histogramm gehört zu einer binomialverteilten Zufallsgröße X.
a) Bestimmen Sie ungefähr \( P(X=\mu) \).
b) Bestimmen Sie das Intervall aller Trefferanzahlen \( \mathrm{k} \), für die gilt:
\( P(X=k) \geq 0,025 \)
c) Begründen Sie, ob nebenstehende Verteilung zu einer binomialverteilten Zufallsvariable mit \( n=240 \) Versuchen und einer Trefferwahrscheinlichkeit \( p=\frac{3}{4} \) gehören kann.
d) Von einer anderen Zufallsgröße \( \mathrm{Y} \) ist der Erwartungswert \( \mu=90 \) sowie \( \sigma= \) gegeben. Berechnen Sie für Y die Anzahl der Versuche \( \mathrm{n} \) und die Trefferwahrscheinlichkeit \( \mathrm{p} \) aus folgendem Ansatz:
\( \begin{array}{r} I: n \cdot p=90 \\ I I: \sqrt{n \cdot p \cdot(1-p)}=6 \end{array} \)
e) Bestimmen Sie zur Zufallsvariablen \( \mathrm{Y} \) das \( 2 \sigma \) - Intervall.
Aufgabe:
Das nebenstehende Histogramm gehört zu einer binomialverteilten Zufallsgröße X.
a) Bestimmen Sie ungefähr \( P(X=\mu) \).
b) Bestimmen Sie das Intervall aller Trefferanzahlen \( \mathrm{k} \), für die gilt:
\( P(X=k) \geq 0,025 \)
c) Begründen Sie, ob nebenstehende Verteilung zu einer binomialverteilten Zufallsvariable mit \( n=240 \) Versuchen und einer Trefferwahrscheinlichkeit \( p=\frac{3}{4} \) gehören kann.
d) Von einer anderen Zufallsgröße \( \mathrm{Y} \) ist der Erwartungswert \( \mu=90 \) sowie \( \sigma= \) gegeben. Berechnen Sie für Y die Anzahl der Versuche \( \mathrm{n} \) und die Trefferwahrscheinlichkeit \( \mathrm{p} \) aus folgendem Ansatz:
\( \begin{array}{r} I: n \cdot p=90 \\ I I: \sqrt{n \cdot p \cdot(1-p)}=6 \end{array} \)
e) Bestimmen Sie zur Zufallsvariablen \( \mathrm{Y} \) das \( 2 \sigma \) - Intervall.
Problem/Ansatz:
Ich war leider krankheitsbedingt 6 Wochen nicht in der Schule und verstehe diese Klausur Aufgabe nicht… bei a) muss man sich doch einfach verschiedene Werte aus dem Diagramm raussuchen und dann denn Erwartungswert ausrechnen?
b) habe ich noch keinen Ansatz
c) einfach n•p nehmen und schauen wie das im Diagramm aussieht?
d) ?
e) einfach das Intervall ausrechnen, das ist mir bewusst.
