Benötige Hilfe bei Dreieckskonstruktion

Question

Moin, bräuchte mal wieder Hilfe bei einer Aufgabe.

Aufgabenstellung:

b) Es gibt zwei Dreiecke, die die Vorgabe b = 7 cm, Alpha = 50°, a = 6 cm erfüllen.
Konstruieren Sie beide Dreiecke und bestimmen Sie die beiden möglichen
Längen der nicht angegeben Seite c!

Problem/Ansatz:

Ich weiß nicht so richtig wie ich die Dreiecke zeichnen soll. Bzw. mit welcher Seite ich anfangen soll. Auch ist mir ehrlich gesagt schleierhaft wieso ich zwei Dreiecke zeichnen soll mit den gleichen Angaben. Über Ideen und eine Hilfestellung wäre ich sehr dankbar da ich auf Youtube und Co nichts in der Richtung gefunden habe was mir weiterhelfen könnte.

Answer 1

Hallo,

zeichne die Strecke \(AC=b\) mit einer Länge von 7cm. Trage dann den Winkel \(\alpha =50°\) (rot) beim Punkt \(A\) an.

Der Kreis um \(C\) mit dem Radius \(a=6\text{cm}\) (schwarz) schneidet den freien Schenkel von \(\alpha\) zweimal in \(B_1\) und \(B_2\). Daher bekommst Du zwei Dreiecke \(AB_1C\) und \(AB_2C\).

Sie stimmen in zwei Seiten und einem Winkel überein, sind aber nicht kongruent.

Gruß Werner

Answer 2

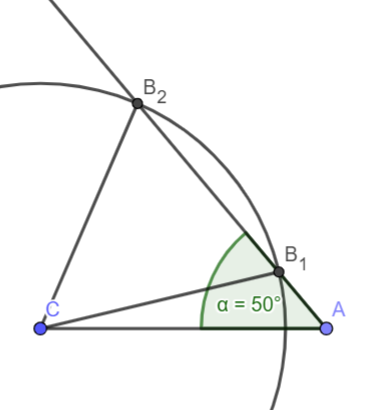
Es gibt zwei Dreiecke, die die Vorgabe b = 7 cm, Alpha = 50°, a = 6 cm erfüllen. Konstruieren Sie beide Dreiecke und bestimmen Sie die beiden möglichen Längen der nicht angegeben Seite c!

Nach Kongruenzsatz Ssw müsste der Winkel der Längeren Seite gegenüberliegen. Das ist hier nicht der Fall daher gibt es zwei Lösungen.

Nach Kosinussatz müsste gelten

6^2 = 7^2 + c^2 - 2·7·c·COS(50°) --> c = 1.808 cm ∨ c = 7.191 cm

Achtung: Für die, die es bewusst missinterpretieren wollen. Mein Gleichheitszeichen bedeutet nicht, dass die Länge exakt der angegebenen entspricht. Ein exakter Ausdruck ist hier deutlich umfangreicher.