Aufgabe:

Text erkannt:
A. 09
Skifahren
a)
Die Geschwindigkeit eines Skifahrers in einem Streckenabschnitt wird durch die Funktion \( v \) beschrieben.
\( v(t)=8+0,2 \cdot t-0,01 \cdot t^{2} \)
\( t \quad \)... Zeit in \( \mathrm{s} \)
\( v(t) \ldots \) Geschwindigkeit zur Zeit \( t \) in \( \mathrm{m} / \mathrm{s} \)
1
- Zeichnen Sie den Graphen der Funktion \( v \) im Intervall \( [0 ; 15] \) in das folgende Koordinatensystem.
4 - Berechnen Sie diejenige Zahl \( b \) aus dem Intervall \( [0 ; 15] \), für die gilt: \( \int \limits_{0}^{b} v(t) \mathrm{d} t=100 \)
Problem/Ansatz:
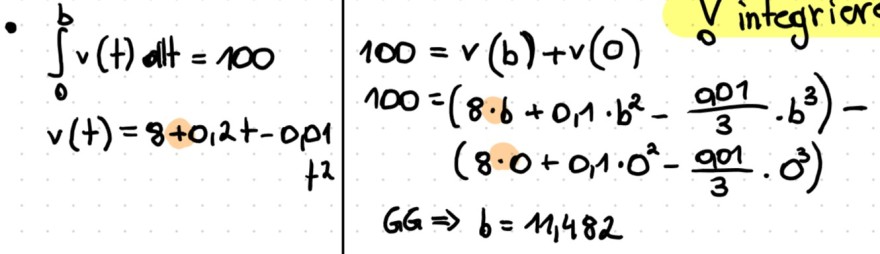
Text erkannt:
\begin{tabular}{r|rl}
\( \int \limits_{0}^{b} v(t) d t=100 \quad 100= \) & \( v(b)+v(0) \quad 0 \) \\
\( v(t)=8+0,2 t-0 p 1 \) & \( =\left(8 \cdot b+0,1 \cdot b^{2}-\frac{901}{3} \cdot b^{3}\right)- \) \\
\( t^{2} \) & \( \left(8 \cdot 0+0,1 \cdot 0^{2}-\frac{901}{3} \cdot 0^{3}\right) \) \\
\( G G \Rightarrow \) & \( b=11,482 \)
\end{tabular}
Bei der Lösung zu der Aufgabe kommt ein * anstatt einem + bei 100 = ....
Ich verstehe nicht ganz warum aus der Addition beim Integrieren plötzlich eine Multiplikation wird...?