Hallo,
berechne zunächst die Extrempunkte von \(f_k(x)\) und dann die Ortskurve.
Zur Kontrolle:
[spoiler]
\(f'_k(x)=e^{kx}\cdot (2x+kx^2)\\H\bigg(-\frac{2}{k}\mid\frac{4}{k^2}\cdot e^{-2}\bigg)\quad T(0\mid 0)\)
Ortskurve: \(g(x)==x^2\cdot e^{-2}\)
[/spoiler]
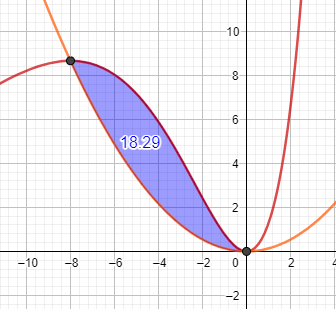
Berechne die Integralgrenzen = x-Koordinaten der Schnittpunkte von \(f_{0,25} \text{ und }g(x)\)
[spoiler]
\(f_{0,25}(x)=x^2\cdot e^{0,25x}\)
\(x^2\cdot e^{0,25x}=x^2\cdot e^{-2}\Rightarrow x_1=-8\quad x_2=0\)
[/spoiler]
Dann benutze deinen Taschenrechner, um das \(\int \limits_{a}^{b}x^2\cdot e^{0,25x}-x^2\cdot e^{-2}\;dx\) zu berechnen.
Gruß, Silvia