Bestimmen Sie alle reellen Zahlen x ∈ ℝ für die Gleichung mit dem Logarithmus

Question

Text erkannt:

Aufgabe 2 [5+5 Punkte]
(a) Bestimmen Sie alle reellen Zahlen \( x \in \mathbb{R} \) für die die Gleichung
\( 2^{\left(3^{x}\right)}=3^{\left(2^{x}\right)} \)
gilt. Hinweis: Ein Ausdruck, der den Logarithmus von gegebenen Zahlen enthält, ist eine gültige Lösung.

Inzwischen habe ich ein Ergebnis ermittelt. Kann das stimmen?

Text erkannt:

a)
\( \begin{aligned} 2^{3^{x}} & =3^{2^{x}} \mid\left(\log _{2}()\right. \\ \log _{2}\left(2^{3^{x}}\right) & =\log _{2}\left(3^{2^{x}}\right) \\ 3^{x} & =\log _{2}\left(3^{2^{x}}\right) \\ 3^{x} & =2^{x} \cdot \log _{2}(3) \mid: 2^{x} \\ \frac{3^{x}}{2^{x}} & =\log _{2}(3) \\ \left(\frac{3}{2}\right)^{x} & =\log _{2}(3) \left\lvert\, \log _{\frac{3}{2}}()\right. \\ x & \left.=\log _{\frac{3}{2}}\left(\frac{\log (3)}{\log (2)}\right) \right\rvert\, \log \operatorname{Gectet} \\ x & =\log _{\frac{3}{2}}(a) \\ x & =\frac{\log (a)}{\log \left(\frac{3}{2}\right)} \\ \Leftrightarrow x & =\frac{\log \left(\frac{\log (3)}{\log (2)}\right)}{\log \left(\frac{3}{2}\right)} \end{aligned} \)

Answer 1

gelöscht

--------------------

Answer 2

Aloha :)

Bei dir wird nach Wegfall von \(\log_2(\cdots)\) aus \(3^x\) ein \(3x\).

Daher ist natürlich auch dein Ergebnis falsch.

$$2^{3^x}=3^{2^x}\quad\big|\ln(\cdots)$$$$\ln(2^{3^x})=\ln(3^{2^x})\quad\big|\ln(a^b)=b\cdot\ln(a)$$$$3^x\cdot\ln(2)=2^x\cdot\ln(3)\quad\big|\div\ln(2)\quad\big|\div2^x$$$$\frac{3^x}{2^x}=\frac{\ln(3)}{\ln(2)}\quad\bigg|\frac{a^c}{b^c}=\left(\frac ab\right)^c$$$$\left(\frac32\right)^x=\frac{\ln(3)}{\ln(2)}\quad\bigg|\ln(\cdots)$$$$x\ln\left(\frac32\right)=\ln\left(\frac{\ln(3)}{\ln(2)}\right)\quad\bigg|\div\ln\left(\frac32\right)$$$$x=\frac{\ln\left(\frac{\ln(3)}{\ln(2)}\right)}{\ln\left(\frac32\right)}\approx1,135882568$$

Comments

Ja das ist mir auch aufgefallen und habe das dann auch sofort wieder rausgenommen, inzwischen habe ich auch eine Lösung ermittelt, die mit deiner übereinstimmt. Vielen Dank

Answer 3

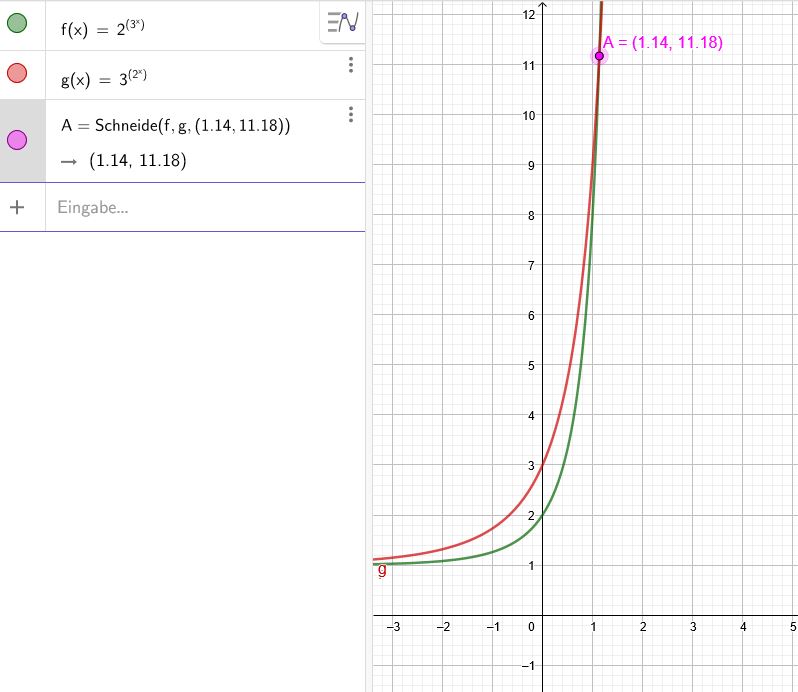
\( 2^{\left(3^{x}\right)}=3^{\left(2^{x}\right)} \)

\( 3^x\cdot ln(2)=2^x\cdot ln(3) \)

\( \frac{3^x}{2^x}=\frac{ln(3)}{ln(2)}\)

\( 1,5^{x}=\frac{ln(3)}{ln(2)} \)

\( x \cdot ln(1,5)=ln(\frac{ln(3)}{ln(2)}) \)

\( x =\frac{ln(\frac{ln(3)}{ln(2)})}{ln(1,5)}≈1,135 \)