Aufgabe: Mathematische Eigenschaften der Rekonstruktion vom Dürer Polyeder.
Problem/Ansatz:
Die Rekonstruktion basiert auf einer Kurve, die scheinbar eine Hyperbel bildet, die allerdings einseitig beschleunigt. Der Beweis für diese Konstruktion lässt sich direkt auf dem Kupferstich am Computer übertragen. Diese Konstruktion hat diverse Interessante Eigenschaften, die ich aber nicht ganz nachvollziehen kann, aufgrund dessen, dass ich mich nur mit Geometrie beschäftige.
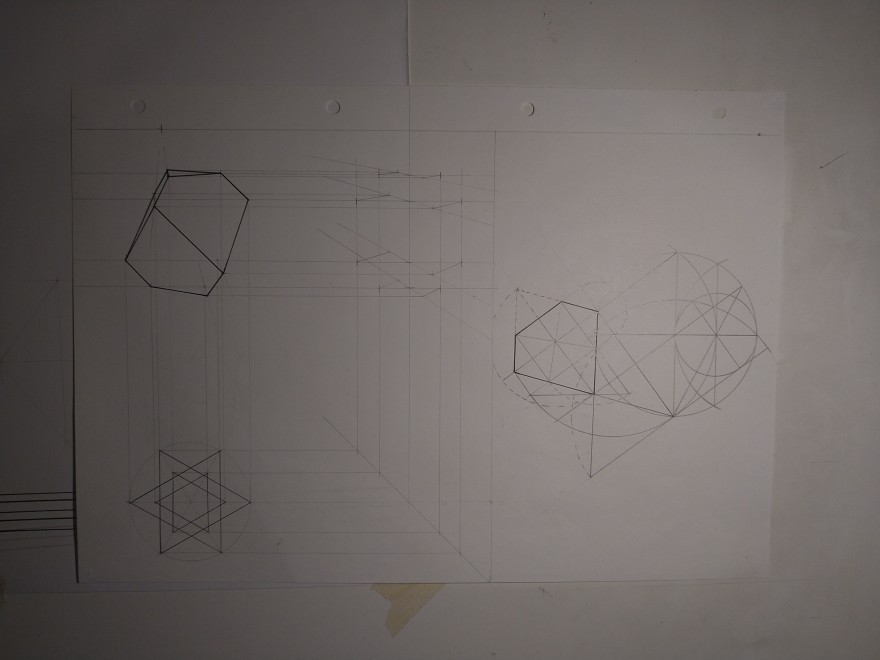
Wenn man bei dem unregelmäßigen Fünfeck an dem Inneren Quadrat ein weiteres Quadrat hinzufügt und eine Gerade vom unteren Eckpunkt des neuen Quadrats durch den unteren Eckpunkt des Fünfeckes konstruiert, dann entsteht ein Schnittpunkt an der Gerade zwischen den beiden Quadraten. Zieht man dann von diesem Punkt eine senkrechte auf die Parallele, die durch den Mittelpunkt des innenliegenden Quadrats geht, trifft man auf den äußeren Punkt des Fünfecks.
Bei laufender Diskussion werde ich noch ein paar Bilder hinzufügen. Eine Zeichnung, die ich mit einer Approximation dessen gemacht habe, wird direkt hinzugefügt.