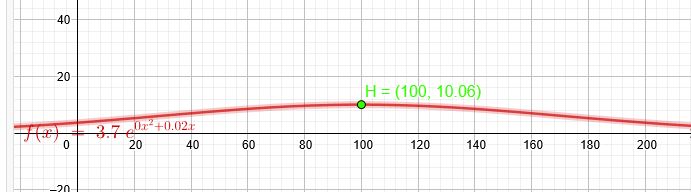
\(g(t)=3,7• e^{-0,0001•t^2 + 0,02•t} \)
\(g'(t)=3,7• e^{-0,0001•t^2 + 0,02•t}•(-0,0002t+0,02) \)
\(3,7• e^{-0,0001•t^2 + 0,02•t}•(-0,0002t+0,02)=0 \)
\(e^{-0,0001•t^2 + 0,02•t}•(-0,0002t+0,02)=0 \)
Satz vom Nullprodukt
\(e^{-0,0001•t^2 + 0,02•t}≠0 \)
\(-0,0002t+0,02=0\)
\(t=100\) \(g(100)=3,7• e^{-0,0001•10000 + 0,02•100}=3,7•e \)