Funktionen: f und ga mit f(x)=1/2x^2 +3x-4 und ga(x)= x^2-a. Gegenseitige Lage von K und Ga?

Question

Hallo hab den a teil von der Aufgabe gelöst und habe eine frage zum b teil.

Aufgabe lautet: Gegeben sind die Funktionen f un g_a durch f(x)=1/2x² +3x-4 und g_a(x)= x²-a.

b) Untersuche Sie die gegenseitige Lage von K und G_a in Abhängigkeit von a.

Meine Lösung ist das 1/2x²-3x+4=a

Aber ich bezweifle das, dass richtig ist. Deshalb wenn es nicht zufällig richtig ist kann mir jemand helfen wie ich auf die Lösung komm. !

MFG

Answer 1

 f(x)=1/2x² +3x-4 und g_a(x)= x²-a.

Du hast hier 2 nach oben geöffnete Parabeln. Wobei f weiter geöffnet ist als g_a

g_a kann mit Hilfe des Parameters vertikal verschoben werden.

Wenn g_a genügend weit unten liegt, schneidet ihr Graph den Graphen von f in 2 Punkten.
Gegenseitige Lage wäre: sich schneidend.

Wenn g_a genügend weit oben liegt, schneidet ihr Graph den Graphen von f überhaupt nicht.
Gegenseitige Lage wäre: punktfremd

Irgendwo in der Mitte gibt es ein a so dass g_a und f genau einen Punkt gemeinsam haben.
Gegenseitige Lage: Sie berühren sich.

Nun muss also das a genauer berechnet werden. Zu unterscheiden sind die Zahl der Schnittstellen. Somit Kurvengleichungen gleichsetzen und dann mit der Diskriminante (vgl. quadratische Gleichungen) arbeiten.

 f(x)=1/2x² +3x-4 und g_a(x)= x²-a.

 1/2x² +3x-4 = x²-a                 |-1/2 x^2 - 3x + 4

0 = 1/2 x^2 - 3x + 4-a                 |*2

0 = x^2 - 6x + 8 -2a       

Diskriminante D = b^2 - 4ac, wobei a=1, b=-6 und c=(8-2a)

D = 36 - 4(8-2a) = 0            |Berührung: D=0

36 - 32 + 8a = 0

8a = -4

a = -1/2                   Berührung

a > -1/2                    2 Schnittpunkte        (vgl. Überlegungen zu Beginn)

a < -1/2                   Kurven sind punktfremd

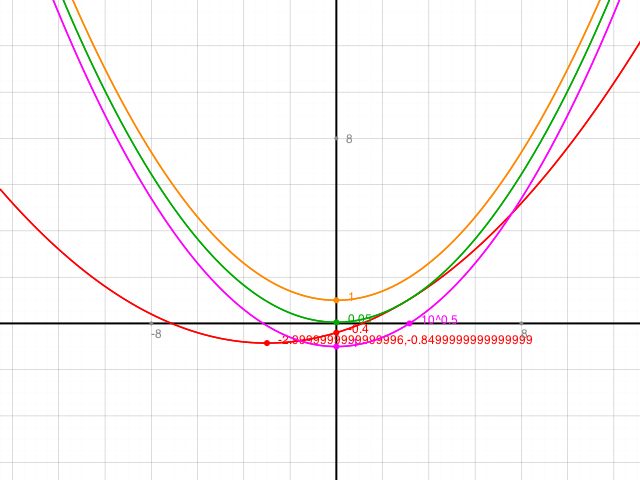
Skizze mit rot: f

grün ist g _-0.5

lila ist g₁₀

gelb ist g _-10

Achung: Plot ist gestaucht um den Faktor 10. D.h. nur auf der y-Achse sind 1 und 8 eigentlich 10 und 80.

Comments

muss ich dann die beide Fkt gleichstellen?

---

aber nicht -a sonder a oder weil wenn du -a rüber holst dann wird es zu + a oder?

---

Ich habe die ja gleichgestellt.
Danach musste ich allerdings nur bis zur Diskriminante weiterrechnen.

Ich habe inzwischen die fragliche Zeile noch ergänzt mit den Rechenschritten.

---

das hab ich jz kapiert aber das wie du auf die -a kommst kapier ich nicht ganz wenn du es rüber ziehst muss es doch +a sein oder?

---

aber wenn du -1/2x²rüberziehst wird es dann nicht zu -1/2x² oder überseh ich da was?

---

x^2 -1/2 x^2 = 1/2 x^2