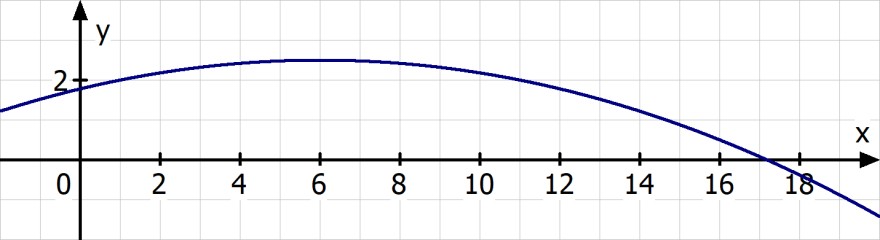
Funktionsgleichung: f(x) = -0,02(x - 6)^2 + 2,5
a) Ergänze den folgenden Satz.
Der Volleyball erreicht nach 6 m seine maximale Höhe von 2,5 m.
Der Schnittpunkt mit der y-Achse ist die Aufschlaghöhe des Balles.
b) Berechne die Aufschlaghöhe des Balles.
f(0) = 1,78
In der Mitte des 18 m langen Spielfeldes steht das Volleyballnetz. Es ist 2,04 m hoch.
c) Fliegt der Ball über das Netz? Begründe deine Antwort mithilfe einer Rechnung.
f(9) = 2,32 → Der Ball fliegt über das Netz.
d) Entscheide mithilfe einer Rechnung, ob der Ball im Spielfeld landet.
f(18) = -0.38 → Der Ball kommt im Feld auf.