Eistee kann Koffeingehalte von bis zu 50 mg pro Glas besitzen. Bei einem Jugendlichen setzt die Wirkung nach einer Stunde ein. Sie nimmt dann mit einer Halbwertszeit von 3 Stunden ab.
a) Wie lautet die Gleichung der Abnahmefunktion K? Skizzieren Sie den Graphen.
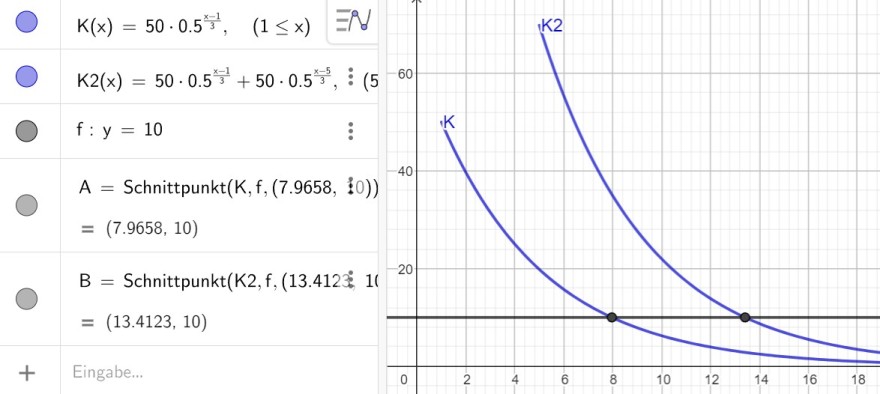
K(t) = 50·0.5^((t - 1)/3)
b) Die anregende Wirkung bleibt erhalten, solange noch 10 mg Koffein im Körper sind. Wie lange ist das der Fall?
K(t) = 50·0.5^((t - 1)/3) ≥ 10 → t ≤ 7.966 h
c) Wie lange dauert der anregende Effekt, wenn die Person nach 4 Stunden ein weiteres Glas Eistee zu sich nimmt?
K2(t) = 50·0.5^((t - 1)/3) + 50·0.5^((t - 5)/3) ≥ 10 → t ≤ 13.412 h
Skizze