Aufgabe:
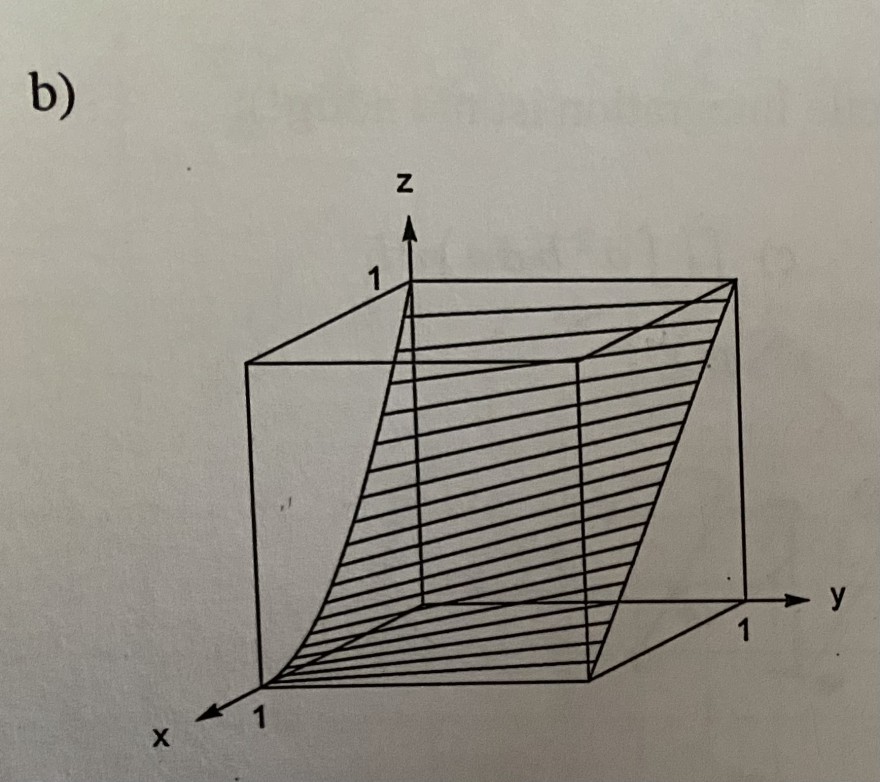
Die nebenstehende Fläche im Würfel mit Kante 1 wird aufgespannt durch zur yz-Ebene parallele Strecken, deren Endpunkte einerseits auf der eingezeichneten Flächendiagonalen und anderseits auf einer Parabel in der xz-Ebene mit Scheitelpunkt (1/0/0) durch den Punkt (0/0/1) liegen.
In welchem Verhältnis wird das Volumen des Würfels durch diese Fläche geteilt?
nebenstehende Fläche:
Text erkannt:
b)
Ansatz:
Da wir im Unterricht das Berechnen von Volumen anhand des Integrals der Querschnittsflächen hatten, dachte ich, dass dies eine solche Aufgabe war. Aber ich konnte diese Aufgabe irgendwie nicht lösen/verstehen.