Ich soll nach dem Kalkül des natürlichen Schliessenshttps://de.wikipedia.org/wiki/Systeme_nat%C3%BCrlichen_Schlie%C3%9Fens#Aussagenlogik beweisen, dass
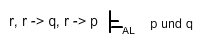
gilt.
Was dasselbe ist, wie
[r und (r -> q) und (r -> p)] -> (p und q)
Semantisch wäre der Beweis ja recht einfach; nehmen wir an, dass "(p und q)" falsch ist, dann muss in den Prämissen "(r -> q)", "(r -> p)" jeweils "r" falsch sein, damit der ganze Ausdruck wahr ist. Nach Voraussetzung muss "r" aber wahr sein, also ist die Annahme falsch und das Inverse der Annahme war, nämlich "(p und q)".
Nun habe ich das mit dem Kaklül des natürlichen Schliessens versucht:
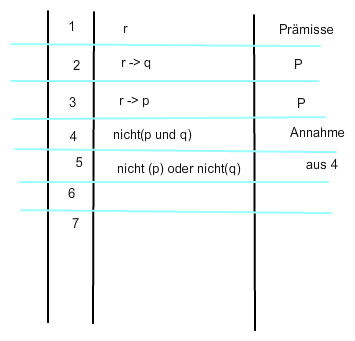
FRAGE:
Wie kriege ich nun die Idee (oben in fett geschrieben) in dieses System hinein?
Danke für eure Hilfe