Berechne das Volumen und die Dachfläche eines Schenkels des Daches.

Question

Aufgabe:

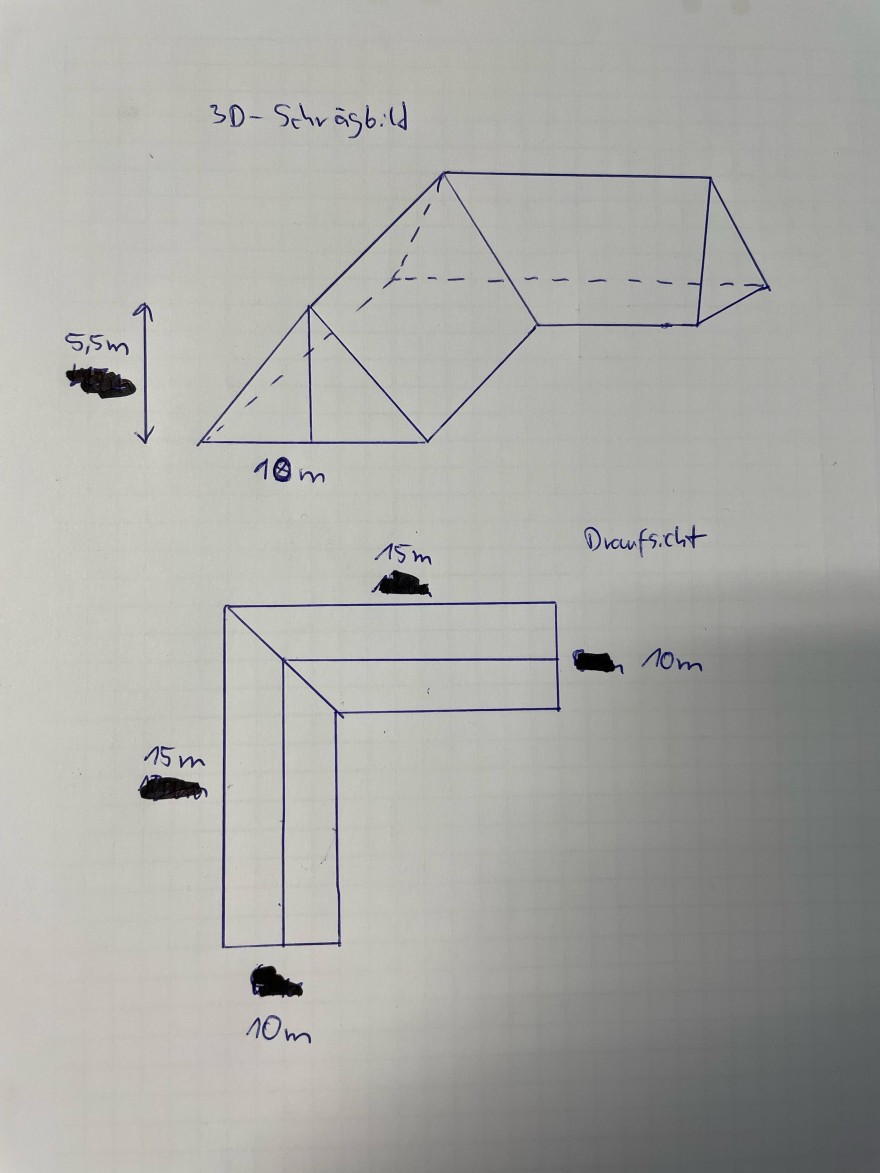
Das Dach bzw. der Dachstuhl eines Gebäudes besteht aus zwei identischen, im 90 Grad-Winkel aneinander grenzenden Schenkeln und hat folgende Form (Siehe Bild). Berechne das Volumen und die Dachfläche eines Schenkels des Daches.

Text erkannt:

3D-Schrägbild

Problem/Ansatz:

Ich verstehe hier leider überhaupt nicht wie ich starten soll. Ich weiß zwar die Formel zur Berechnung der Fläche eines Trapezes, aber ich kann die zu berechnenden Flächen hier einfach nicht erkennen. Ich habe viele Werte vorgegeben, aber habe schon drei unterschiedliche Ergebnisse berechnet (94,5m² / 130,5m² / 81m²). Ich kann auch nicht beurteilen, ob diese überhaupt richtig sind. Kann mir da jemand mal einen guten Ansatz geben?

Answer 1

Ich denke, folgende Skizze hilft dir die einzelnen Teile besser zu erkennen, um die es geht. Ich habe das jetzt nach deinen Bemaßungen gezeichnet. Du siehst, dass entweder deine Bemaßung falsch ist oder deine Skizze nicht Maßstabsgerecht ist. Das solltest du evtl. auch vor dem Ausrechnen klären.

Comments

Okay danke, das hilft mir auf jeden Fall die Formen besser zu erkennen. Wie starte ich jetzt am besten, diese Flächen und das Volumen zu berechnen?

---

Die Flächen sind doch einfache Trapeze. Die Länge der unteren und der oberen Seite kannst du jeweils ohne Rechnung sagen. Für die Höhe musst du den Pythagoras bemühen.

Für das Volumen hast du einmal ein Dreiecksprisma und zwei schiefe Dreieckspyramieden.

Die rechte schiefe Dreieckspyramide ist auch eine Halbe Pyramide, wenn dir das einfacher fällt.

---

Bitte sorgfältig kontrollieren:

V = 275 m³

A = 10·√221 = 148.7 m²

---

Perfekt, danke!

Am Flächeninhalt habe ich mich eben einmal versucht. Da komme ich tatsächlich jetzt auch auf 148,6m². Das Volumen berechne ich dann später nochmal.

---

Ich habe noch eine Frage zu dem Volumen: Ich habe das Volumen von dem Dreiecksprisma wie folgt ausgerechnet:

V = 0,5 x Grundfläche x Höhe x Länge

V = 0,5 x 10m x 5,5m x 5m

V = 137,5m³

Bei den schiefen Dreieckspyramiden stehe ich aber noch total auf dem Schlauch, welche Formel kann ich dafür verwenden?

---

Das ist richtig. Bedenke aber das die Formel falsch ist

V = Grundfläche * Körperhöhe mit

Grundfläche = 1/2 * g * h = 0.5 * 10 * 5.5 und Körperhöhe = 5

Das Volumen einer Pyramide ist

V = 1/3 * Grundfläche mal Körperhöhe. Die Körperhöhe ist dabei der Abstand der Pyramidenspitze von der Grundfläche.