Formel der Totalen Wahrscheinlichkeit, fehlendes Verständnis

Question

Formel der Totalen Wahrscheinlichkeit, fehlendes Verständnis

Aufgabe:

In einer Bankfiliale befinden sich ein alter und ein neuer Geldautomat. Die
Wahrscheinlichkeit, dass der ältere an einem Tag ausfällt (Ereignis A), beträgt 40 %. Der neuere fällt mit der Wahrscheinlichkeit 10 % aus (Ereignis B). Beide Automaten fallen an einem Tag mit der Wahrscheinlichkeit
5 % aus.

a) Wie groß ist die Wahrscheinlichkeit, dass mindestens einer an einem
Tag ausfällt?
b) Mit welcher Wahrscheinlichkeit funktionieren beide Automaten an einem Tag?
c) Wie groß ist die Wahrscheinlichkeit, dass der neue Automat ausfällt,
wenn der alte ausgefallen ist?

d) Wie groß ist die Wahrscheinlichkeit, dass der neue Automat ausfällt,
wenn der alte nicht ausfällt?( hier hängts siehe weiter unten)

Problem/Ansatz:

Ich habe A-C lösen können. Die D verstehe bis zu einem gewissen grad teil 1.png

Text erkannt:

$ P(A)=0,4 \quad P(B)=0,1 \quad P(A \cap B)=0,05 $
a) Es muss also das Ereignis A oder B oder beide eintreten. Gesucht ist also die Wahrscheinlichkeit der Vereinigung der Ereignisse:
$ P(A \cup B)=P(A)+P(B)-P(A \cap B)=0,4+0,1-0,05=0,45 $
b) Hierbei handelt es sich um das Gegenereignis zu a):
$ P(\overline{A \cup B})=1-P(A \cup B)=0,55 $
c) Hierfür benötigen wir die Definition der bedingten Wahrscheinlichkeit:
$ P(B \mid A)=\frac{P(B \cap A)}{P(A)}=\frac{P(A \cap B)}{P(A)}=\frac{0,05}{0,4}=0,125 $

Bis hierhin war mir alles klar, ich habe dazu folgende Formel genutzt: Satz des Bayes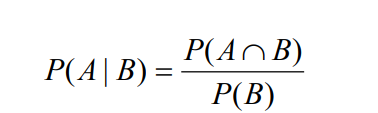 Teil 2.png

Text erkannt:

$ P(A \mid B)=\frac{P(A \cap B)}{P(B)} $

In der D wird nun die Formel der Totalen Wahrscheinlichkeit benötigt:

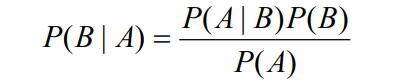
teil 3.png

Text erkannt:

$ P(B \mid A)=\frac{P(A \mid B) P(B)}{P(A)} $

Die Formel sieht übersichtlich aus. Die Rechnung sieht aber alles andere als übersichtlich aus

teil 4.png

Text erkannt:

d) Gesucht ist $ P(B \mid \bar{A}) $. Da uns $ P(A) $, und damit auch $ P(\bar{A}), P(B) $ und $ P(B \mid A) $ bekannt sind, setzen wir gemäß der Formel der totalen Wahrscheinlichkeit an:
$ \begin{aligned} P(B) & =P(B \mid A) \cdot P(A)+P(B \mid \bar{A}) \cdot P(\bar{A}) \Rightarrow P(B \mid \bar{A})=\frac{P(B)-P(B \mid A) \cdot P(A)}{P(\bar{A})} \\ & =\frac{0,1-0,125 \cdot 0,4}{0,6}=0,083 \end{aligned} $

Mir ist bewusst das wir A Strich suchen unter der Bedingung das B nicht eintritt. Aber wenn ich mir dann die Rechnung angucke verstehe ich gar nichts. Nach welchen Prinzip hat man links die Zahlen aufgeschrieben und nach welchen Prinzip hat man dann rechts die Gleichung mit dem Bruchstrich aufgestellt?Ich was, was die Sachen bedeuten, ich weiß aber nicht ,wie man das ganze anordnet.

Gefragt 1 Jul von DerHorst

📘 Siehe "Statistik" im Wiki

2 Antworten

Beste Antwort

Die von dir angegebene Formel ist nicht die von der totalen Wahrscheinlichkeit, sondern der Satz von Bayes.

Text erkannt:$ P(B \mid A)=\frac{P(A \mid B) P(B)}{P(A)} $

Die Formel für die totale Wahrscheinlichkeit eines Ereignisses lautet

$P(B)=P(B|A)P(A) + P(B|\overline{A})P(\overline{A})$.

Daraus ergibt sich durch einfaches Auflösen nach der gesuchten Wahrscheinlichkeit

$P(B|\overline{A})=\frac{P(B)-P(B|A)P(A)}{P(\overline{A})}$.

Es lässt sich auch die Definition der bedingten Wahrscheinlichkeit direkt anwenden:

$P(B|\overline{A})=\frac{P(B\cap \overline{A})}{P(\overline{A})}$.

Nun ist aber $P(B\cap\overline{A})$ die Wahrscheinlichkeit, dass $B$ und nicht $A$ zeitgleich eintreten, also

$P(B\cap\overline{A})=P(B)-P(B\cap A)=P(B)-P(B|A)P(A)$

nach Multiplikationssatz.

Die für diese Aufgabe benötigten Zahlen wurden alle zuvor schon ermittelt und stehen bereits in deiner Lösung.

Mir ist bewusst das wir A Strich suchen unter der Bedingung das B nicht eintritt.

Gesucht ist $B$ unter der Bedingung, dass $A$ nicht eintritt.

Beantwortet 1 Jul von Apfelmännchen

Ein anderes Problem?

Stell deine Frage

Der_Mathecoach · Answer 1 · 2024-07-01T20:56:16+0000

KI:

Gegeben:
P(A) = 0,40 (Wahrscheinlichkeit, dass der alte Automat ausfällt)
P(B) = 0,10 (Wahrscheinlichkeit, dass der neue Automat ausfällt)
P(A ∩ B) = 0,05 (Wahrscheinlichkeit, dass beide Automaten ausfallen)
a) Die Wahrscheinlichkeit, dass mindestens einer ausfällt, ist:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
= 0,40 + 0,10 - 0,05 = 0,45 oder 45%
b) Die Wahrscheinlichkeit, dass beide funktionieren, ist das Gegenereignis zu a):
P(beide funktionieren) = 1 - P(A ∪ B) = 1 - 0,45 = 0,55 oder 55%
c) Die bedingte Wahrscheinlichkeit, dass der neue ausfällt, wenn der alte ausgefallen ist:
P(B|A) = P(A ∩ B) / P(A) = 0,05 / 0,40 = 0,125 oder 12,5%
d) Die Wahrscheinlichkeit, dass der neue Automat ausfällt, wenn der alte nicht ausfällt:
Hier verwenden wir die bedingte Wahrscheinlichkeit: P(B|nicht A)

Zuerst berechnen wir P(nicht A) = 1 - P(A) = 1 - 0,40 = 0,60
Dann berechnen wir P(B ∩ nicht A):
P(B ∩ nicht A) = P(B) - P(A ∩ B) = 0,10 - 0,05 = 0,05
Nun können wir die bedingte Wahrscheinlichkeit berechnen:
P(B|nicht A) = P(B ∩ nicht A) / P(nicht A)
= 0,05 / 0,60
= 0,0833 oder etwa 8,33%

Also beträgt die Wahrscheinlichkeit, dass der neue Automat ausfällt, wenn der alte nicht ausfällt, etwa 8,33%.

Kommentiert 2 Jul von ggT22

Die Nutzung von KI ist ja auch nicht verkehrt. Man sollte das aber nicht 1 zu 1 abschreiben.

Ich denke das, was hier noch verteufelt wird, ist die teilweise noch schlechte Qualität bei den automatisch generierten Antworten und die mathematischen Ungenauigkeiten. Es fehlt hier schlicht die Prüfung auf Korrektheit. Und jetzt neuerdings auch die Aktion, einfach selbst KI-Antworten zu erzeugen und ohne groß darüber nachzudenken sämtliche Fragen damit vollzuspammen. Die KI könnte jeder FS selbst bedienen und sich damit befassen. Einige tun das ja sogar schon. Das Forum sollte doch eine Plattform sein, wo es weiterhin "menschliche Unterstützung" gibt. Insofern ist die Einschränkung der automatisch KI-generierten Antworten bei sehr alten Fragen sinnvoll, da die Wahrscheinlichkeit einer Rückmeldung des FS eher gering ist, man mit derartigen Fragen aber durchaus auch die KI testen kann.

Kommentiert 2 Jul von Apfelmännchen

Ich habe es zwar noch nicht probiert, aber vermutlich kann man die KI auch bewegen eine Vierfeldertafel zum Problem zu notieren.

Und ja, kann man:

Hier ist die Vierfeldertafel (Kontingenztafel) für die Ereignisse $ A $ (der ältere Automat fällt aus) und $ B $ (der neuere Automat fällt aus):

$$ \begin{array}{c|c|c|c} & B & \neg B & \text{Summe} \\ \hline A & 0.05 & 0.35 & 0.40 \\ \hline \neg A & 0.05 & 0.55 & 0.60 \\ \hline \text{Summe} & 0.10 & 0.90 & 1.00 \\ \end{array} $$

### Erklärung:
- $ A $: Der ältere Automat fällt aus.
- $ \neg A $: Der ältere Automat fällt nicht aus.
- $ B $: Der neuere Automat fällt aus.
- $ \neg B $: Der neuere Automat fällt nicht aus.

- $ P(A) = 0.40 $: Wahrscheinlichkeit, dass der ältere Automat ausfällt.
- $ P(B) = 0.10 $: Wahrscheinlichkeit, dass der neuere Automat ausfällt.
- $ P(A \cap B) = 0.05 $: Wahrscheinlichkeit, dass beide Automaten gleichzeitig ausfallen.

Die restlichen Wahrscheinlichkeiten werden durch Subtraktion berechnet:
- $ P(A \cap \neg B) = P(A) - P(A \cap B) = 0.40 - 0.05 = 0.35 $
- $ P(\neg A \cap B) = P(B) - P(A \cap B) = 0.10 - 0.05 = 0.05 $
- $ P(\neg A \cap \neg B) = 1 - P(A) - P(B) + P(A \cap B) = 1 - 0.40 - 0.10 + 0.05 = 0.55 $

So ergibt sich die vollständige Vierfeldertafel.

Kommentiert 2 Jul von Apfelmännchen

Formel der Totalen Wahrscheinlichkeit, fehlendes Verständnis

2 Antworten

Ähnliche Fragen

Eingabetools:

Beliebte Fragen:

Heiße Lounge-Fragen: