Könnte erklären, wie ich auf K* und L* komme?

Question

Text erkannt:

14:47 Montag 15. Juli
- \( 100 \%[4 \)
[1.
Copy of Öbung 1
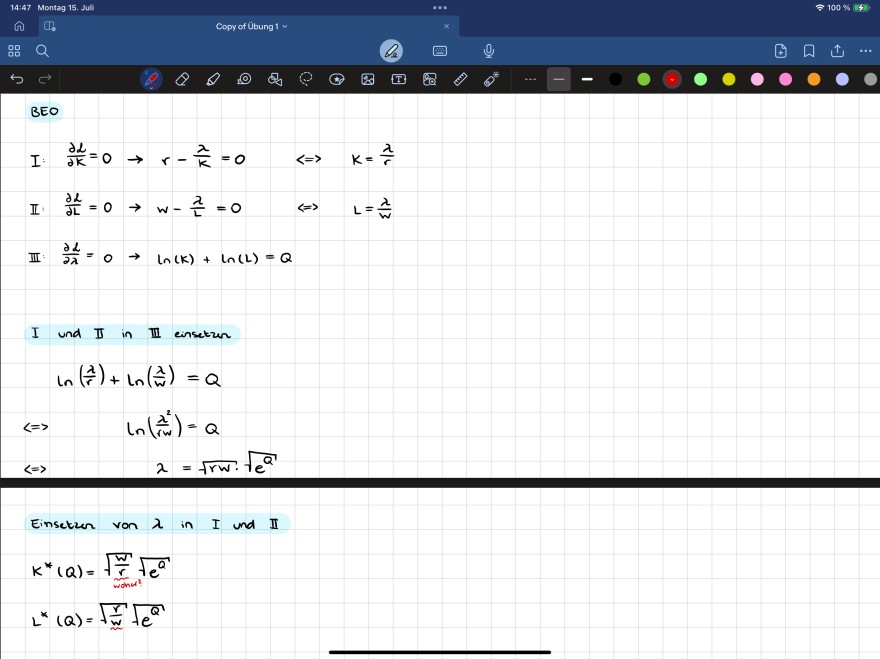
BEO
I: \( \frac{\partial \mathcal{L}}{\partial K}=0 \rightarrow r-\frac{\lambda}{K}=0 \quad \Leftrightarrow \quad K=\frac{\lambda}{r} \)
II. \( \frac{\partial L}{\partial L}=0 \quad \rightarrow w-\frac{\lambda}{L}=0 \quad \Leftrightarrow \quad L=\frac{\lambda}{w} \)

III: \( \frac{\partial L}{\partial \lambda}=0 \rightarrow \ln (k)+\ln (L)=Q \)

I und II in III einsetzen
\( \begin{aligned} \ln \left(\frac{\lambda}{r}\right)+\ln \left(\frac{\lambda}{w}\right) & =Q \\ \Leftrightarrow \quad \ln \left(\frac{\lambda^{2}}{r w}\right) & =Q \\ \Leftrightarrow \quad \lambda & =\sqrt{r w} \cdot \sqrt{e^{Q}} \end{aligned} \)

Einsetzen von \( \lambda \) in \( I \) und \( I I \)
\( \begin{array}{l} K^{*}(Q)=\sqrt{\frac{w}{r}} \sqrt{e^{Q} u^{2}} \\ L^{*}(Q)=\sqrt{\frac{r}{w}} \sqrt{e^{Q}} \end{array} \)

Könnte mir bitte jemand erklären, wie ich auf K* und L* komme? Ich verstehe nicht, wie die Lösungen zustande kommen, wenn ich Landa bei I und II einsetze.

Answer 1

Hier wurden nur Potenz-/Wurzelgesetze verwendet.

\(K^*(Q)=\frac{\lambda}{r}=\frac{\sqrt{rw}\sqrt{\mathrm{e}^Q}}{r}=\frac{\sqrt{r}\sqrt{w}\sqrt{\mathrm{e}^Q}}{r}=\frac{\sqrt{w}\sqrt{\mathrm{e}^Q}}{\sqrt{r}}=\sqrt{\frac{w}{r}}\sqrt{\mathrm{e}^Q}\).

Allgemein gilt: \(\displaystyle\frac{\sqrt{x}}{x}=\frac{x^{\frac{1}{2}}}{x^1}=x^{\frac{1}{2}-1}=x^{-\frac{1}{2}}=\frac{1}{x^{\frac{1}{2}}}=\frac{1}{\sqrt{x}}\) (das wurde bei der vorletzten Gleichung angewendet)

Answer 2

Ich hoffe, so ist das etwas klarer.

K = λ/r

mit λ = √(r·w·e^Q)

K = √(r·w·e^Q)/r

K = √(r·w·e^Q/r^2)

K = √(w·e^Q/r)

Comments

Allgemein gilt:

$$\frac{\sqrt{x}}{x} = \frac{\sqrt{x}}{\sqrt{x} \cdot \sqrt{x}} = \frac{1}{\sqrt{x}}$$