Aufgabe:
Hallo,
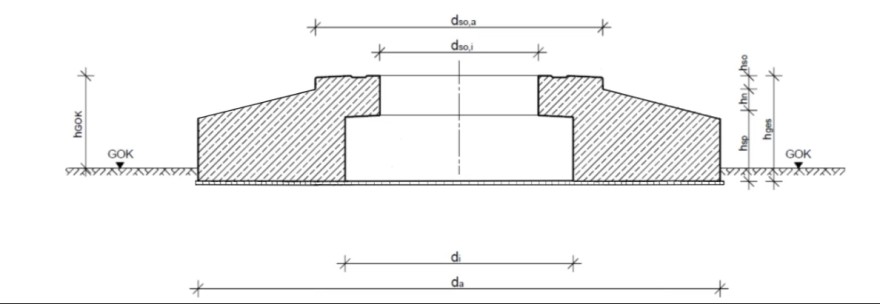
ich möchte gerne von einem Kreisringfundament das Volumen berechnen (s. System mit den blauen Linien bzw. das untere Bild). Ich habe zunächst das Fundament in 3 Teilstücken aufgeteilt. In 2 Rechtecke und einem Dreieck.
Die zwei Rechtecke habe ich mit der Formel für einen Hohlzylinder berechnet.
Problem/Ansatz:
Nun habe ich das Problem die Dreiecksteile zu berechnen.
Meine Idee war es:
1.Ein "Ersatzzylinder" (in grau) zu erstellen
2. Volumen des Ersatzzylinders berechnen
3. Zur vereinfachung habe ich mir nur die eine hälfte des Systems angeschaut (Symmetrie)
4. Das Verhältnis der einzelnen Längen zur Gesamtlänge des halbierten Systems berechnet (21,50m/2)=10,75m und diesen Prozentwert dann mal dem Gesamtvolumen des halben Systems berechnet
5. Am Ende habe ich von dem dritten Volumenanteil die Hälfte genommen, da es sich ja um ein Dreieck handelt und nicht um ein gesamten Rechteck wie im Ersatzsystem
Meine Frage ist, ob es so richtig wäre zu rechnen? Darf man rückschlüsse auf den Anteil der Länge auf das Volumen ziehen?
Gibt es sonst eine andere Möglichkeit das Volumen des Kreisringfundaments zu berechnen?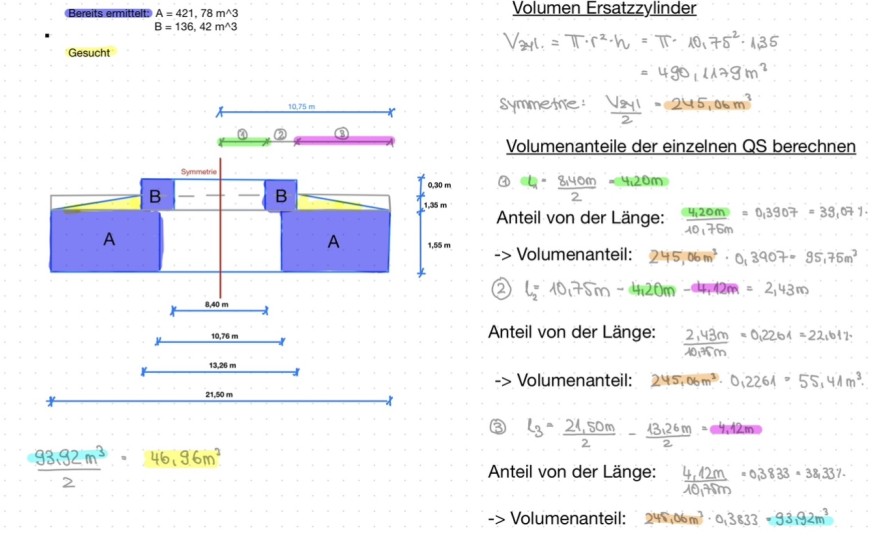
Text erkannt:
Bereits ermittelt: \( A=421,78 \mathrm{~m}^{\wedge} 3 \)
\( B=136,42 \mathrm{~m}^{\wedge} 3 \)
Gesucht
\( \frac{93.92 m^{3}}{2} \cdot 46.96 m^{2} \)
Volumen Ersatzzylinder
\( \begin{aligned} V_{z 1}=\pi \cdot r^{2} \cdot h & =\pi \cdot 10,75^{2}: 1,35 \\ & =490,1179 \mathrm{~m}^{3} \end{aligned} \)
symmetrie: \( \quad \frac{V_{2 y 1}}{2}=245,06 \mathrm{~m}^{3} \)
Volumenanteile der einzelnen QS berechnen
(4) \( 4: \frac{8,40 m}{2}-4,20 \mathrm{~m} \)
Anteil von der Länge: \( \frac{4,20 \mathrm{~m}}{10,76 \mathrm{~m}}=0,3907=39,071 \).
\( -> \) Volumenanteil: \( 245,06 \mathrm{~m}^{3}: 0,3907 \cdot 95,75 \mathrm{~m}^{2} \)
(2) \( l_{2}=10,75 m-4,20 m-4,42 m=2,43 m \)
Anteil von der Länge: \( \quad \frac{2,43 \mathrm{~m}}{10,35 \mathrm{~m}}=0,2261=22,61 \% \)
-> Volumenanteil: \( \quad 245,06 \mathrm{~m}^{3} \cdot 0,2261=55,41 \mathrm{~m}^{3} \).
(3) \( l_{3}=\frac{21,50 m}{2}-\frac{13,26 m}{2}=4,12 \mathrm{~m} \)
Anteil von der Länge: \( \frac{4,12 m}{10,75 m}=0,3833=38,33 \% \)
\( \rightarrow \) Volumenanteil: \( \quad 245,06 m^{3} \cdot 0,3833=93,92 m^{3} \)
Text erkannt:
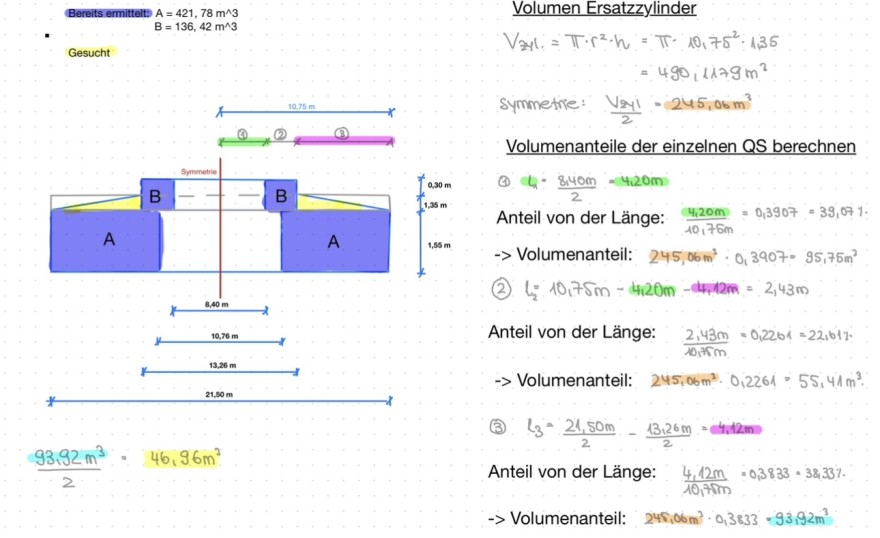
Bereits ermittelt: \( A=421,78 \mathrm{~m}^{\wedge} 3 \)
\( B=136,42 \mathrm{~m}^{\wedge} 3 \)
Gesucht
\( \frac{93.92 m^{3}}{2} \cdot 46.96 m^{2} \)
Volumen Ersatzzylinder
\( \begin{aligned} V_{z 1}=\pi \cdot r^{2} \cdot h & =\pi \cdot 10,75^{2}: 1,35 \\ & =490,1179 \mathrm{~m}^{3} \end{aligned} \)
symmetrie: \( \quad \frac{V_{2 y 1}}{2}=245,06 \mathrm{~m}^{3} \)
Volumenanteile der einzelnen QS berechnen
(4) \( 4: \frac{8,40 m}{2}-4,20 \mathrm{~m} \)
Anteil von der Länge: \( \frac{4,20 \mathrm{~m}}{10,76 \mathrm{~m}}=0,3907=39,071 \).
\( -> \) Volumenanteil: \( 245,06 \mathrm{~m}^{3}: 0,3907 \cdot 95,75 \mathrm{~m}^{2} \)
(2) \( l_{2}=10,75 m-4,20 m-4,42 m=2,43 m \)
Anteil von der Länge: \( \quad \frac{2,43 \mathrm{~m}}{10,35 \mathrm{~m}}=0,2261=22,61 \% \)
-> Volumenanteil: \( \quad 245,06 \mathrm{~m}^{3} \cdot 0,2261=55,41 \mathrm{~m}^{3} \).
(3) \( l_{3}=\frac{21,50 m}{2}-\frac{13,26 m}{2}=4,12 \mathrm{~m} \)
Anteil von der Länge: \( \frac{4,12 m}{10,75 m}=0,3833=38,33 \% \)
\( \rightarrow \) Volumenanteil: \( \quad 245,06 m^{3} \cdot 0,3833=93,92 m^{3} \)