Hallo,
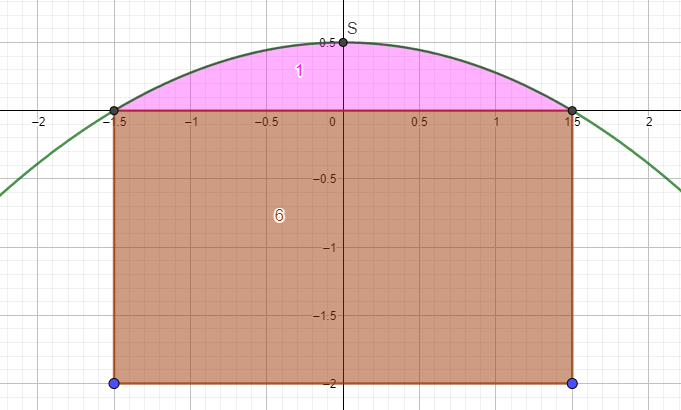
bei einer Funktion der Form \(f(x)=ax^2+bx+c\) bezeichnet c die Verschiebung der Parabel entlang der y-Achse. Hier ist also c = 0,5.
Du kennst zudem zwei weitere Punkte (Nullstellen) der Funktion, mit denen du a und b bestimmen kannst, indem du deren Koordinaten einsetzt.
\(f(x)=ax^2+bx+c\\ 2,25a+1,5b+0,5=0\\ \underline {2,25a-1,5b+0,5=0}\\ 4,5a+1=0\Rightarrow a =-\frac{2}{9}\)
Um den Flächeninhalt der Vorderseite des Hauses zu bestimmen, berechnest du den Flächeninhalt des Integrals zwischen den Nullstellen plus der rechteckigen Fläche.
Bei einer anderen Aufgabe würdest du dein Ergebnis noch mit der Tiefe des Häuschens/Körpers multiplizieren.
Gruß, Silvia