Hallo,
Du hast eigentlich zwei Fragen gestellt, einmal nach den Winkeln im Trapez und einmal nach der Eindeutigkeit des Trapez. Ich denke, ersteres ist Dein eigentliches Anliegen. So wie döschwo die Winkel aus Deiner Skizze oben berechnet hat, ist das nur möglich, wenn man die Koordinaten der einzelnen Punkte kennt. Zum Beispiel von dem Punkt (6|1) oben rechts, usw. Das ist i.A. natürlich nicht der Fall, dann hat man ja nur die Seitenlängen.
Man kann die Winkel im Trapez berechnen, wenn man ein Parallelogramm der Breite c abscheidet, so dass man ein Dreieck erhält. So wie in dieser Zeichnung
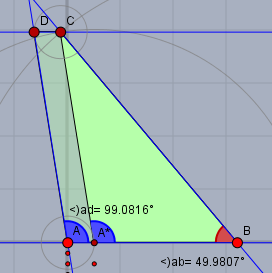
Trage dazu einen Punkt \(A^*\) auf \(AB\) ab,, so dass \(|AA^*|=c\) ist. Dann erhält man das Dreieck \(\triangle A^*BC\) mit dem Winkel \(\angle BA^*C=\alpha\) (blau) und \(\angle CBA^*=\beta\) (rot). Da \(|A^*C|=d\) sind alle Seiten dieses Dreiecks bekannt und man kann die Winkel mit Hilfe des Kosinussatzes berechnen.
Der lautet:$$w^2 = u^2+v^2 - 2uv\cos(\varphi)$$ (Bem.: ich habe hier andere Bezeichner \(u,v,w\) für die Seiten des Dreiecks gewählt, um Dich nicht zu verwirren!)
\(w\) ist die Seite, die dem zu berechnenden Winkel gegenüber liegt. Und \(u\) und \(v\) sind die Seiten, die den Winkel einschließen. Wenn man also \(\alpha\) berechnen möchte, ist in diesem konkreten Fall$$w = b \quad u = d\quad v = |A^*B|= a-c \\ b^2 = d^2 + (a-c)^2 - 2d(a-c) \cos(\alpha)$$löst man diese Gleichung nach \(\cos(\alpha)\) auf, so lässt sich der Winkel \(\alpha\) berechnen.
Ich habe Dir dafür ein Desmos-Script erstellt, welches diese Berechnung durchführt:
Klicke rechts unten im Bild auf das Desmos-Symbol. Dann öffnet sich die Webseite des Graphik-Rechners und Du kannst oben links in der Seite auch andere Werte für die Seiten eintragen.
Gruß Werner