Es könnte sein, dass die Aufgabenstellung nicht so sehr auf das explizite Berechnen der Flächeninhalte anhand der Koordinaten abzielt.
Deshalb hier noch ein anderer Lösungsvorschlag:
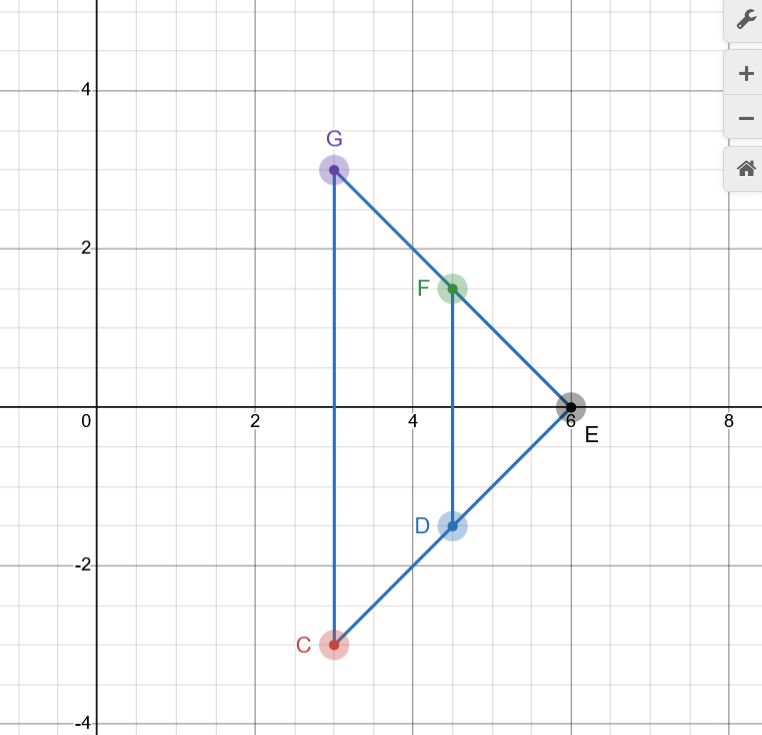
\(\triangle{CEG}\) und \(\triangle{DEF}\) sind ähnlich. Dabei kannst du an der x-Achse ablesen, dass \(\triangle{CEG}\) aus \(\triangle{DEF}\) hervorgeht, indem vom Streckzentrum E aus mit dem \(\color{blue}\text{Faktor }2\) gestreckt wird. (Du kannt auch mit dem Strahlensatz argumentieren.)
Damit gilt für die Flächen der beiden Dreiecke:
$$A_{\triangle{CEG}} = {\color{blue}\text{2}}^2\cdot A_{\triangle{DEF}} = 4\cdot A_{\triangle{DEF}}$$
Nun erhältst du die Fläche des Trapezes als Vielfaches der Dreiecksfläche durch Abziehen:
$$\begin{array}{rcl}A_{CDFG} & = & A_{\triangle{CEG}} - A_{\triangle{DEF}} \\ & = & 4A_{\triangle{DEF}}- A_{\triangle{DEF}} \\ & = &3A_{\triangle{DEF}}\end{array}$$