Seien E und F Ereignisse einer Ergebnismenge Ω. Zeige, dass P(¬E/F)=1-P(E/F) gilt.

Question

kann mir hier einer bei helfen?

1) Seien E und F Ereignisse einer Ergebnismenge Ω. Zeigen sie das P(¬E/F)=1-P(E/F) gilt

und

2) Seien A und B zwei unabhängige Ereignisse einer Ergebnismenge Ω mit P(A)>0 und P(B)>0. Zeigen Sie, dass dann auch gilt
P(B/¬A)=P(B),
P(A,¬B)= P(A) und
P(¬A/¬B)=P(¬A)

Danke

Anmerkung: P(B) > 0 . Korrigiert (Lu).

Comments

Zu 2. Hast du das richtig hingeschrieben?

P(B) < 0 kommt bei Wahrscheinlichkeiten nicht in Frage.

---

Die Ungleichung ist korrigiert. Die Behauptung bei 2. mit Zeilenumbrüchen ergänzt. Nur: Was bedeuten die Kommas? ,
Stehen die für 'und' / Schnittmenge?

EDIT: JotEs hat Recht. unabhängig genügt vollauf, wenn ein Komma für 'unter der Bedingung von' steht.

---

also bis auf diesen einen Fehler steht die Aufgabe genau so auf dem Blatt, auch mit den , . Eventuell soll man das für alle drei Ereignisse zeigen? Darunter steht noch: Beweisen Sie, dass das unmögliche Ereignis 0 und das sichere Ereignis (Omega) unabhängig von jedem beliebigen Ereignis A c (soll dieses und bzw. oder Zeichen zur Seite sein) Omega sind. Aber das hat ja im eigentlichen Sinne nichts mit der anderen Aufgabe zu tun oder?

---

A c (soll dieses und bzw. oder Zeichen zur Seite sein) Omega

Es handelt sich um das Zeichen für eine Teilmenge. 

 

Und so ganz verstehe ich die Diskussion um die Aufgabenstellung nicht. Es scheint mir völlig klar zu sein, dass sowohl die Behauptung

P(B/¬A)=P(B),

als auch die Behauptung

P(A/¬B)= P(A)
(hier ist dem Fragesteller wohl ein Komma, statt eines Schrägstriches hineingeraten)

als auch die Behauptung

P(¬A/¬B)=P(¬A)

gezeigt werden soll.

Answer 1

zu 1)

Betrachte folgende Skizze:

 

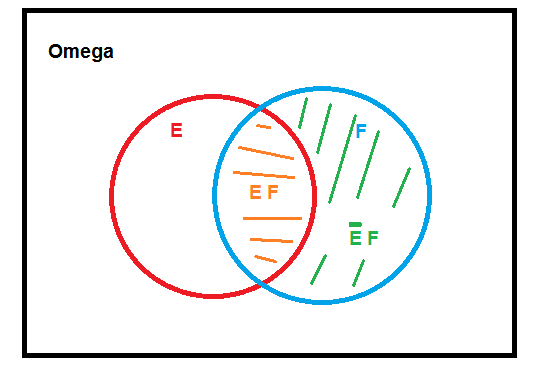
Das schwarz umrandete ist die Ergebnismenge Omega, das rot umrandete das Ereignis E und das blau umrandete das Ereignis F.

Die Schnittmenge von E und F ( in der Skizze als E F geschrieben) ist orange schraffiert, während die Schnittmenge von ¬ E und F ( in der Skizze als E F  mit einem Strich über dem E geschrieben) grün schraffiert ist.

Offensichtlich gilt:

F = ( E ∩ F ) ∪ ( ¬ E ∩ F )

sowie:

( E ∩ F ) ∩ ( ¬ E ∩ F ) = ∅

Die beiden Teilmengen E ∩ F und ¬ E ∩ F sind also disjunkt. Daher gilt:

P ( F ) = P ( E ∩ F ) + P ( ¬ E ∩ F )

[ Division durch P ( F ) : ]

<=> 1 = [ P ( E ∩ F ) / P ( F ) ] + [ P ( ¬ E ∩ F ) / P ( F ) ]

[ Schaut man sich nun die Definition der bedingten Wahrscheinlichkeit an:

P ( A | B ) = P ( A ∩ B ) / P ( B ) 

so sieht man, dass man die Ausdrücke

P ( E ∩ F ) / P ( F ) als P ( E | F )

bzw.

P ( ¬ E ∩ F ) / P ( F ) als P ( ¬ E | F )

schreiben kann, also: ]

<=> 1 = P ( E | F ) + P ( ¬ E | F )

<=> P ( E | F ) = 1 - P ( ¬ E | F )

q.e.d.

 

zu 2)  Hier musst du die Aufgabenstellung noch einmal überarbeiten (siehe Kommentar von Lu).

 

EDIT: (nach Klarstellung):

A, B sind stochastisch unabhängig <=> P ( A ∩ B ) = P ( A ) * P ( B ) 

Damit ergibt sich für die laut Aufgabenstellung stochastisch unabhängigen Ereignisse A und B:

P ( B / ¬ A ) = P ( B ∩ ¬ A ) / P ( ¬ A ) = P ( B ) * P (¬ A ) / P (¬ A ) = P ( B )

sowie

P( A |¬ B ) = P ( A ∩ ¬ B ) / P ( ¬ B ) = P ( A ) * P (¬ B ) / P (¬ B ) = P ( A )

sowie:

P ( ¬ A / ¬ B ) = P ( ¬ A ∩ ¬ B ) / P ( ¬ B ) = P ( ¬ A ) * P (¬ B ) / P (¬ B ) = P ( ¬ A )

Comments

Ihr habt recht, Schreibfehler. sollte heissen P(A)>0 und P(B)>0 Danke

---

Ich habe nun auch Teil 2 beantwortet.

---

Vielen lieben Dank, ich war leicht verwirrt wegen dem hin und her der Fragestellung. Aber dank deiner Erklärung ist es klar. Danke