5. (Geradengleichungen) Gegeben sind zwei Geraden in \( \mathbf{R}^{2} \) :
\( g_{1}: x_{1}-2 x_{2}=0 \quad \text { und } \quad g_{2}: 4 x_{1}+2 x_{2}=5 \)
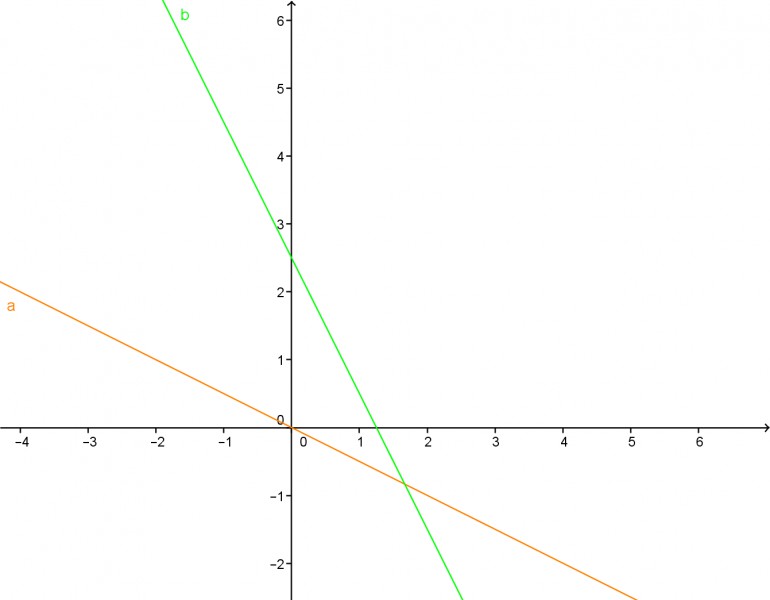
(a) Zeichnen Sie die Geraden in einem Koordinatensystem mit den Koordinaten \( x_{1} \) und \( x_{2} . \) Bringen Sie dazu die Geradengleichungen durch Auflösen nach \( x_{2} \) in die Ihnen bekannte funktionale Form \( y=m x+b\left(x_{2}\right. \) spielt also die Rolle von \( y, x_{1} \) die von \( x \) ).
(b) Berechnen Sie den Schnittpunkt der beiden Geraden.
(c) In welchen Punkten schneidet \( g_{3}: 2 x_{1}+x_{2}=5 \) die Geraden \( g_{1} \) und \( g_{2} \) ?
(d) Betrachten Sie nun noch die Geradenschar \( g_{4}(b):-x_{1}+b x_{2}=1 \). Wie muss \( b \) gewählt werden, damit sich die drei Geraden \( g_{1}, g_{2} \) und \( g_{4} \) in einem Punkt schneiden?
Lösungen:
\( g_{1}: x_{1}-2 x_{2}=0 \)
\( g_{2}: 4 x_{1}+2 x_{2}=5 \)
Umschreibung: \( x_{1}=x \) und \( x_{2}=y \) \( g_{1}: x-2 y=0 \)
\( g_{2}: 4 x+2 y=5 \)
\( g_{1}: x-2 y=0 \quad \mid-x \)
\( g_{1}:-2 y=0-x \quad \mid:(-2) \)
\( g_{1}: y=0-\frac{x}{2} \)
\( g_{1}: y=-\frac{x}{2}+0 \)
\( g_{2}: 4 x+2 y=5 \quad \mid-4 x \)
\( g_{2}: 2 y=5-4 x \mid:(2) \)
\( g_{2}: y=-2 x+\frac{5}{2} \)
b)
Gleichungssystem:
I: -2·m + b = 5/2
II: -1/2·m + b = 0
I - II: -3/2·m = 5/2 | :(-3/2)
m = -5/3
in II: -1/2·(-5/3) + b = 0 b = 0 - (-1/2)·(-5/3) = -5/6
Gesuchte Funktion: f(x) = -5/3·x-5/6
S(-5/3 |+5/6)