Unter welchem Sehwinkel erscheint die Kugel?

Question

Vor dem Beobachter liegen eine Kugel und eine Kreisscheibe, beide vom Durchmesser 1.0m. Die Entfernung Auge – Mittelpunkt ist jeweils 1.50m.

a) Unter welchem Sehwinkel erscheint die Kugel?

b) Unter welchem Sehwinkel erscheint die Scheibe, wenn der Beobachter senkrecht darauf schaut?

Answer 1

Nun, bei der Kreisscheibe gilt:

tan ( alpha / 2 ) = 0,5 / 1,5
<=> alpha / 2 = arctan ( 0,5 / 1,5 )

<=> alpha = 2 * arctan ( 0,5 / 1,5 ) ≈ 36,87 °

Bei der Kugel hingegen gilt:

sin ( alpha / 2 ) = 0,5 / 1,5
<=> alpha / 2 = arcsin ( 0,5 / 1,5 )

<=> alpha = 2 * arcsin ( 0,5 / 1,5 ) ≈ 38,94 °


Ich fertige gleich noch eine Skizze dazu an.

Hier ist sie:

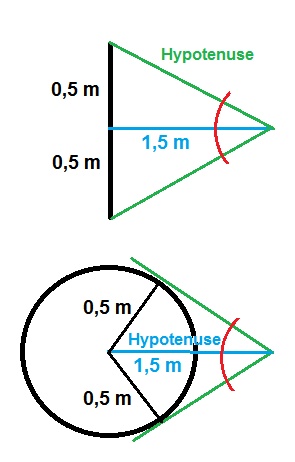
Beachte die in den beiden Fällen unterschiedliche Lage der Hypotenuse. Daraus ergibt sich, dass man bei der Kreisscheibe mit dem Tangens, bei der Kugel jedoch mit dem Sinus des Blickwinkels rechnen muss.