wenn die Zahlen so stimmen, kannst Du ja den Scheitelpunkt (0|3,60) in die Funktionsgleichung einsetzen:
3,60 = -a*02 + c
Also ist c = 3,60
Da die Spannweite insgesamt 20m beträgt, hat man außerdem
-a*102 + 3,60 = 0 | -3,60
-a*102 = -3,60 | : 102
-a = -3,60/102 = -0,036
Damit lautet die Funktionsgleichung
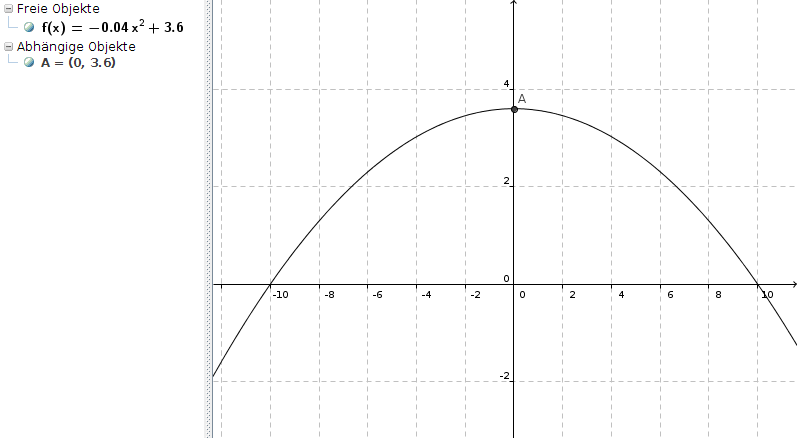
y = -0,036x2 + 3,60
Besten Gruß