Question

Die Dichte einer stetig verteilten Zufallsvariablen X sei

f(x)= 0 für x <= 1

(x-1) hoch 2 für 1<= x <=2

-3/4x + 5/2 für 2<=x<=10/3

0 für x >= 10/3

das alles gilt für f(x)= { (nur in groß, leider hier nicht darstellbar)

a) skizzieren sie f(x)

 dann soll man die dazugehörige verteilungsfunktion bestimmen und skizzieren und dann noch E(X) berechnen.

kann mir hier irgendeiner bei helfen?
Vielen lieben Dank dafür.

Answer 1

Ich zeichne mal beide Graphen

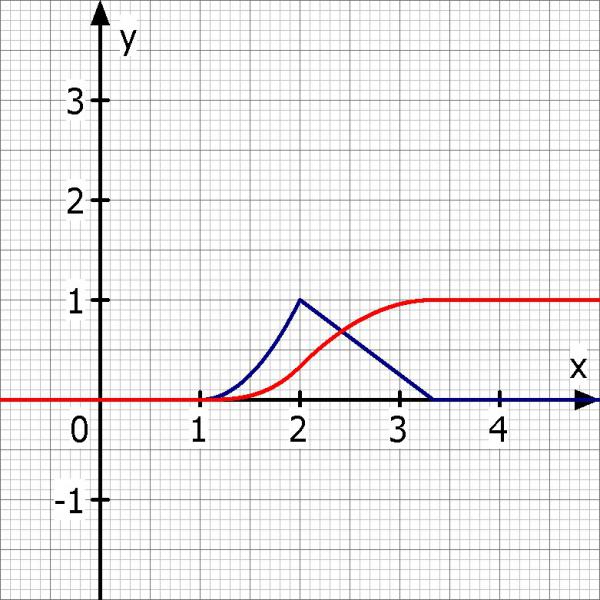
Hier definiere ich die Verteilungsfunktion. Intervalle sind die gleichen wie in der Dichtefunktion.

f(x) = 0
f(x) = (x - 1)^3/3
f(x) = - 3*x^2/8 + 5*x/2 - 19/6
f(x) = 1

E(X) = ∫(x·(x - 1)^2, x, 1, 2) + ∫(x·(- 3/4·x + 5/2), x, 2, 10/3) = 7/12 + 44/27 = 239/108 = 2.213

Comments

Das ist nett danke, aber kannst du ein wenig erklären was du dort tust?
Danke

---

Die Verteilungsfunktion ist eine Integralfunktion für die Dichtefunktion.

Ansonsten sag was du nicht verstehst.

---

Der rote Graph ist f(x) oder?
Ansonsten kann ich deine Rechnung leider nicht so ganz nachvollziehen.

vielen Dank für deine Bemühungen.

---

ich kann deine Rechnungen bei f(x) nicht nachvollziehen. Kannst du da vielleicht mal nur eine als Beispiel ausschreiben? Danke

---

Du mist die Dichtefunktion Integrieren

f(x) = (x - 1)^2

F(x) = 1/3*(x - 1)^3

Diese Stammfunktion muss man noch anpassen das sie am Intervallbeginn den richtigen Wert hat. Das wäre hier aber eh der Fall.

---

ist das richtig das blau der graph von f(x) ist und rot der von der Verteilungsfunktion?

---

Ja. Das sollte so sein.

---

War mir nicht ganz sicher, danke schön