Berechnung von Grenzwerten: bn = (n^2+5) / √( n^4 - n^3)

Question

Ich schreibe dienstag meine Mathe Klausur und wir müssen die Grenzwertberechnung drauf haben. Gucke schon seid Tagen Videos an komme einfach nicht weiter.

Hier die Aufgabenszellung:

Gegeben ist die Folge bn, die auf Konvergenz untersucht werden soll:

n^2+5/ wurzel aus n^4 - n^3

aus wurzel n^3 steht auf einmal wurzel 1-1/2 n

 

Wäre nett wenn Ihr mir helfen Könntet

Anm(Lu) Vermute, dass es hier um

$${ b }_{ n }=\frac { { n }^{ 2 }+5 }{ { \sqrt { { n }^{ 4 }{ -n }^{ 3 } }  } } $$

geht.

{ b }_{ n }=\frac { { n }^{ 2 }+5 }{ { \sqrt { { n }^{ 4 }{ -n }^{ 3 } }  } } 

Answer 1

Es ist leider gar nicht klar, wie dein b_n aussieht. Ich rate mal etwas, das Sinn machen würde, und forme Schritt für Schritt um.

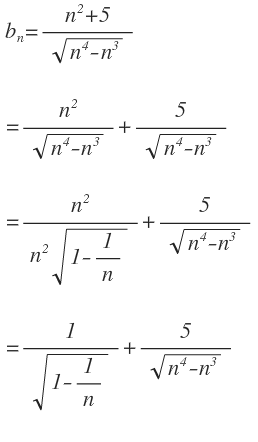
Wenn man hier n----> unendlich betrachtet gilt:

Der erste Summand wird zu 1/√1 = 1.

Der zweite Summand wird zu 0

Grenzwert von bn für n gegen unendlich ist somit 1.

 

Exkurs

An der Stelle, wo n² vor die Wurzel kommt, benutze ich

n⁴ = (n²)²

und

n³ = n⁴/n = n⁴ * 1/n

Daher gilt n⁴ + n³ = n⁴ (1 + 1/n)

n⁴ kann man nun als n² vor die Wurzel schreiben. 

 

Das ist noch der Text zur Formeleingabe (Falls du auch mal eine Formel eingeben möchtest):

{ b }_{ n }=\frac { { n }^{ 2 }+5 }{ { \sqrt { { n }^{ 4 }{ -n }^{ 3 } }  } } \\ \\ =\frac { { n }^{ 2 } }{ { \sqrt { { n }^{ 4 }{ -n }^{ 3 } }  } } +\frac { 5 }{ { \sqrt { { n }^{ 4 }{ -n }^{ 3 } }  } } \\ \\ =\frac { { n }^{ 2 } }{ { { n }^{ 2 }\sqrt { 1-\frac { 1 }{ n }  }  } } +\frac { 5 }{ { \sqrt { { n }^{ 4 }{ -n }^{ 3 } }  } } \\ \\ =\frac { 1 }{ { \sqrt { 1-\frac { 1 }{ n }  }  } } +\frac { 5 }{ { \sqrt { { n }^{ 4 }{ -n }^{ 3 } }  } } \\