Funktion zur Dauer einer Fahrt im Riesenrad bestimmen

Question

Das größte Riesenrad der Welt, das London Eye, hat einen Durchmesser von 135 Meter, für eine volle Umdrehung benötigt es 20 Minuten.

a) Ermitteln Sie die Funktion s, die der Zeit t nach dem Einsteigen die Höhe über dem Boden zuordnet. Führen Sie hierzu ein geeignetes Koordinatensystem ein.

b) Zeichnen Sie mit Verwendung des GTR den Graphen der Funktion s.

c) In welcher Höhe befindet man sich sieben Minuten nach dem Einsteigen?

d) Wie viel Zeit ist seit dem Einsteigen vergangen, wenn man 100 Meter über dem Boden ist?

Ansatz:

Ich habe daraus f(x)=-1.35x(x-20) gemacht. Darf man das?

Answer 1

Hallo immai,

 

wenn man von einer quadratischen Funktion ausgeht, gilt allgemein

f(x) = ax² + bx + c

Hier hat man gegeben

I. f(0) = 0 = c | Beginn einer Fahrt

II. f(10) = 135 = 100a + 10b | Nach 10 Minuten ganz oben

III. f(20) = 0 = 400a + 20b | Nach 20 Minuten wieder am Ausgangspunkt

4 * II = III

400a + 40b - 540 = 400a + 20b

20b = 540

b = 27

In II

135 = 100a + 270

-135 = 100a

a = -1,35

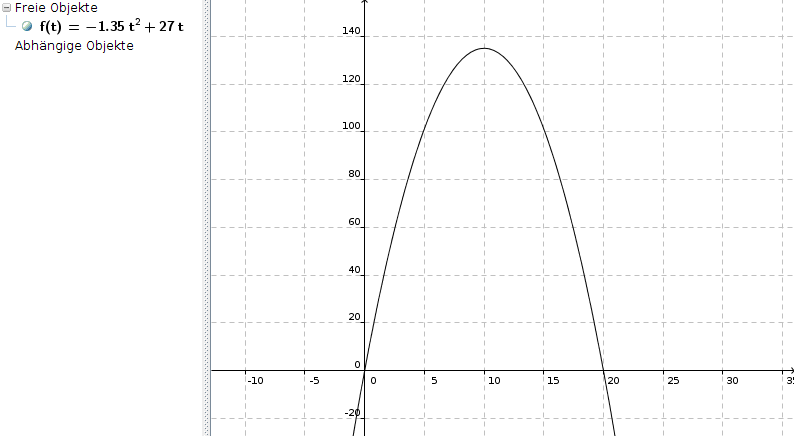
f(t) = -1,35t² + 27t

Das entspricht Deiner Lösung.

Diese kann aber nicht korrekt sein, weil man sich nach dieser Funktionsgleichung nach 5 Minuten schon in einer Höhe von 101,25 Metern befinden würde, tatsächlich müssen es aber 135/2 Meter = 67,50 Meter sein (siehe Skizze)

 

Wie man auf die (wahrscheinlich richtige) Alternativlösung kommt, kann ich Dir leider im Moment auch nicht sagen.

EDIT:

Dazu nur folgende Idee:

Beim Einheitskreis hat man für 270° den sin-Wert -1, beim Riesenrad hat man die Höhe 0 bei 0°;

wenn man jetzt im Gegenzeigersinn weiter geht, hat man für 360° bzw. 0° den sin-Wert 0, beim Riesenrad hat man die Höhe 67,50 Meter bei 90°;

für 90° hat man den sin-Wert 1, beim Riesenrad die Höhe 135 Meter bei 180° usw.

Das muss man jetzt "nur noch" geschickt miteinander verbinden.

 

Besten Gruß