(9-x²)^{1/2} ableiten

Question

wie kann ich (9-x²)^(1/2) ableiten ohne diese als Wurzelfunktion anzugeben also √(9-x²). Bei der Wurzelfunktion würde ich die Kettenregel anwenden. Wie wird eine Funktion abgeleitet, wenn im Exponent ein Bruch steht?

Answer 1

 

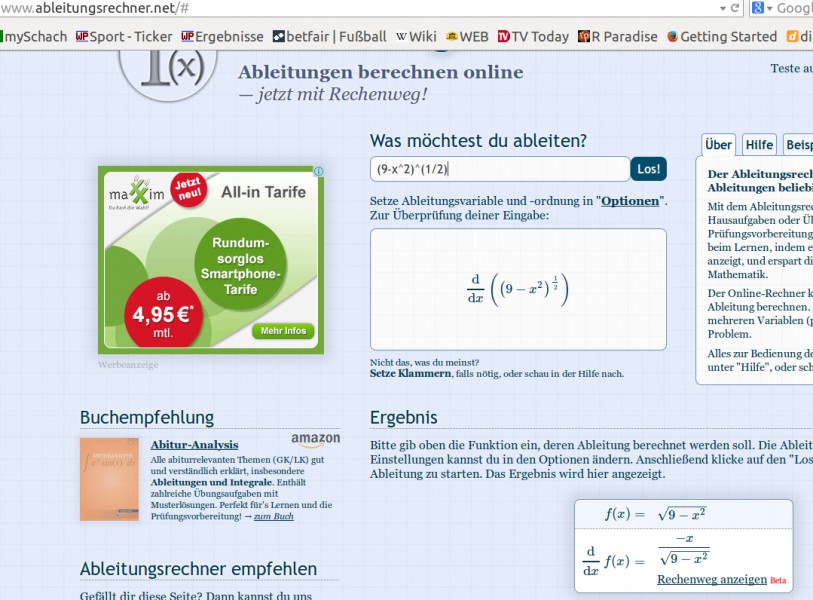
man rechnet innere Ableitung * äußere Ableitung.

Die innere Funktion ist hier

9 - x² mit der Ableitung -2x.

Die äußere Funktion ist

x^1/2 mit der Ableitung 1/2 * x^-1/2

(Hierbei wird der Term innerhalb der Klammer - statt x haben wir eben 9 - x² - unverändert gelassen.)

Insgesamt also

f(x) = (9 - x²)^1/2

f'(x) = -2x * 1/2 * (9 - x²)^-1/2 =

-x * (9 - x²)^-1/2 =

-x / √(9 - x²)

 

 

Besten Gruß

Answer 2

Das ist die Ableitung -x/(wurzel(9-x^2))

du hast ja ja 1/2 als exponent den holst du runter und machst mal der inneren Ableitung was ja -2x ist dann kürzt sich die die -2 weg und du hast im Zähler -x dann musst du beachten das du ja die 1/2 runter geholt hast also musst du im exponent einen weniger machen also(9-x^2) 1/2-1 was ja minus 1/2 im exponent heist das heist du hast (9-x^2)^-1/2

also kannst du auch statt Minus 1/2 1/2 in den Nenner schmeißen und die wurzel dafür schreiben

Answer 3

(-2x)(1/2)(9-x^2)^{-1/2}. Noch fragen? Hochzahl runter mal innere. Hochzahl minus 1.