Hallo Ihr Lieben,
ich habe zu einigen Fragen zu Aufgaben aus dem Themen Bereich der Quadratischen Gleichungen, und würde jetzt einmal gerne alle Fragen in einer Frage stellen, damit es nicht zu viel wird.... Ich würde mich sehr über eure Hilfe freuen, Danke im Vorhinaus :)
1. Frage; Sind folgende Gleichungen richtig aufgelöst wurden?
1) x2+21x+20=0
pq-Formel:
p=21
q=20
x1/2=-(21/2) +- √(21/2)2-20)
=-10,5+-√(90,259
=-10,5+-9,5
x1= -10,5+9,5=-1
x2= -10,5-9,5= -20
2) x2-3x+2=0
pq-Formel:
p=-3x
q=+2
x1/2=-((-3)/2) +- √(((-3)/2)2 -2)
=1,5+-√(2,25-2)
=1,5+-√(0,25)
=1,5+-0,5
x1=1,5+0,5=2
x2=1,5-0,5=1
2. Anwendung von Quadratischen Gleichungen:
1) Das rechteckige Grundstück im Bild ist vererbt wurden. Die neuen Eigentümer wollen die Rasenfläche belassen und das restliche Grundstück wie angeben in zwei gleich große Teile zerlegen.
Wie groß ist jedes Teilstück?
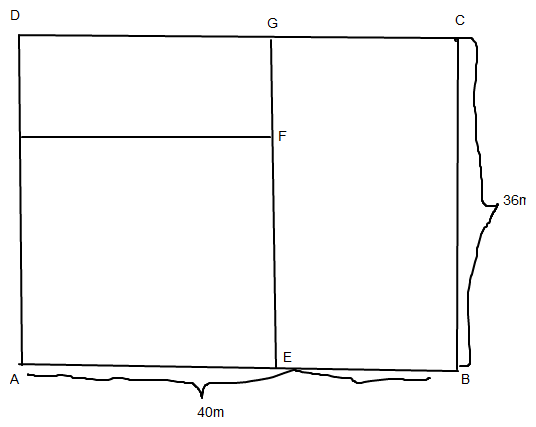
1-> Variable festlegen
x=Länge der Quadratseiten
2-> Gleichung
Flächeninhalt Quadrat=Flächeninhalt Rechteck
Q = R
x2=36*(40-x)
Ich würde gerne wissen ob mein Ansatz bei folgender Aufgabe richtig ist oder ob ich so daneben liege, das ich gar nicht erst Rechnen sollte?
2) Wenn man bei einem Quadrat die eine Seitenlänge verdoppelt, die benachtbarte um 5 cm verringert, so erhält man ein Rechteck, dessen Fläche um 24cm2 größer ist als die Fläche des Quadrates. Welche Seitenlänge hat das Quadrat?
Rechnung:
Quadrat wir in ein Rechteck umgewandelt
Seitenlänge Quadrat= x
Flächeninhalt Quadrat= x2
Seitenlänge Rechteck=2x und x-5
Flächeninhalt Rechteck= 2x (x-5)
->Differenz: 24cm2
Rechteck-Quadrat=Differenz (wird grösser)
2x(x-5)-x2=24
x2-10x-24=0
x1/2= 5+-√(25+24)=5+-7
x1=12
(x2=-2) -> negativ also keine wirkliche Lösung
Probe am Text:
Seitenlänge Quadrat: 12cm
Flächeninhalt Quadrat: (12)2=144cm2
Seitenlänge Rechteck: a=2*12=24cm; b=12cm-5cm=7cm
Flächeninhalt Rechteck: 7cm*24cm=168cm^2
Bei dieser Aufgabe bin ich mir trotz der Probe am Text total unsicher... Ich würde mich Freuen wenn jemand einmal drüber schaut und mir bei Fehlern helfen können, also auf den Fehler hinweisen und genau erklären, wo mein Fehler liegt, Danke im Vorhinaus :)
3) Gegeben ist ein Rechteck mit den Seitenlängen 6cm und 5cm
Verkürze alle Seiten um jeweils dieselbe Länge, sodass der Flächeninhalt 2/3 des ursprünglichen Inhalts beträgt.
Bestimme die neue Seitenlänge
Seitenlänge Rechteck: 6 und 5
Verkürzung der Seitenlänge: 6-x und 5-x
"alt" Flächeninhalt ursprünglich Rechteck: 6*5=30
"neu" Flächeninhalt nach der Verkürzung (6-x) (5-x)
Flächeninhalt "neu" = 2/3 vom Flächeninhalt "alt"
(6-x)(5-x)=2/3*30
Habe ich denn Ansatz richtig und wenn Ja, wie geht es weiter?
3. Ich habe noch eine Aufgabe zum Thema Quadratische Gleichungen, bei der ich noch nicht einmal den Ansatz hinbekommen, es würde mir schon sehr helfen, wenn ihr mir nur eine kleine Starthilfe mit dem Ansatz gegen könntet, damit ich dann weiter Rechnen kann, Danke im Vorhinaus :)
Rechteck und Trapez sollen denselben Flächeninhalt besitzen. Wie lang müssen die Seiten des Rechtecks sowie die Grundseiten des Trapezes sein?
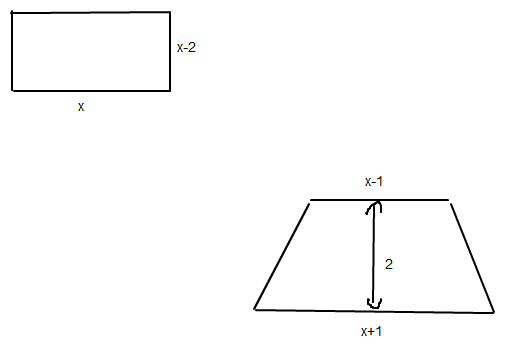
Ich bedanke mich schon einmal gaaanz lieb für eure tolle Hilfe:)
Und ich hoffe ihr seit mir nicht böse, wenn die Zeichnungen etwas unordentlich und nicht ganz den normalen normen der Mathematischen Regeln entsprechend sind
LG elena