Heute ging es früh raus für unser Team. Es wurde von 09:50 bis 20:00 Uhr geradelt. Sie trafen auf haushohe Bäume, mussten Steigungen von bis zu 12 % meistern und trafen auf den See Loch Ness!
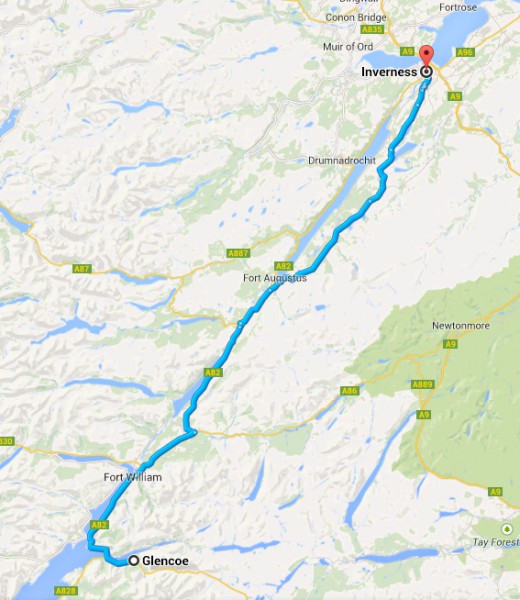
Die lange Fahrt von 129 km führte von Glencoe bis Inverness:
Ein Foto vom wunderschönen See Loch Ness:

Und hier ein Eindruck von den Bäumen:

Mathe-Challenge (leicht):
Als unsere Radler in Inverness ankamen, verschlug es sie auch gleich in eine der lokalen Whisky-Bars, wo sie an einer Degustation teilnehmen durften:

Am Ende der Verkostung pustete einer der Biker in ein Alkoholtestgerät, es zeigte 1,3 Promille an, worauf er sagte, "Ich hab 6 Liter Blut im Körper, davon sind 13 ml reiner Alkohol!". Prüfe, ob er wirklich 13 ml Alkohol im Blut hat. Wir gehen davon aus, dass sich tatsächlich 6 Liter Blut in seinem Körper befinden. (PS: Nicht nachmachen, Whisky ist erst ab 18 Jahren erlaubt.)
Lösung Mathe-Challenge Tag 11:
Die Tageslänge soll mit der Formel f(x) = a*sin(bx) + d angenähert werden. Gegeben waren drei spezifische Tage für die Tageslängen in Berlin (ohne Berücksichtigung von Schaltjahren):
1. mittlere Tageslänge mit 12 Stunden am 21.03. (also 80. Tag des jahres)
2. längster Tag mit 16,5 Stunden am 21.06. (also 172. Tag des Jahres) → Maximum
3. kürzester Tag mit 7,5 Stunden am 21.12. (also 355. Tag des Jahres). → Minimum
Gesucht ist die Gleichung der Sinusfunktion, die diese Werte annimmt. Wir gehen wie folgt vor:
- Maximum bei f(172) = 16,5 h
- Minimum bei f(355) = 7,5 h
- die mittlere Tageslänge d ist: d = (y_max + y_min) / 2 = (16,5 + 7,5) / 2 = 12 h
- Amplitude a = (y_max - y_min) / 2 = (16,5 - 7,5) / 2 = 4,5 h
- Periodenlänge p war gegeben mit 1 Jahr = 365 Tage, demnach gilt für b = 2 PI / p = 2 PI / 365 ≈ 0,0172
- Funktionsgleichung mit Werten aufstellen:
f(x) = a*sin(bx) + d
f(x) = 4,5*sin(0,0172*x) + 12
Nun gilt es noch, die Tageslänge für den 15.09. mit Hilfe der Formel zu bestimmen. Der 15.09. ist der 258. Tag im Jahr. Diesen setzen wir in die Formel ein und erhalten: f(258) = 4,5*sin(0,0172*258) + 12 ≈ 12,35 Stunden, das sind 12 h und 21 min. Ein Blick auf die tatsächlichen Daten verrät uns: 12 h 39 min, wir erhalten also einigermaßen diesen Wert (Differenz 18 min).