Funktionsschar Nullstellen Symmetrie: fa(x)=x^3-3a^2 x+2a^3

Question

Folgendes: Ich habe die Funktionsschar f_a(x)=x³-3a²x+2a³

Ich soll nun zeigen, dass alle Graphen der Schar die x-Achse berühren und dass f_a symmetrisch zu f_-a ist. 

 Wie stelle ich so etwas an?

Comments

Hast du richtig abgeschrieben? f_-a geht aus f_a durch eine Parallelverschiebung um -4a^3 hervor. (Nicht Symmetrie)

f_a(x)=x³-3a²x+2a³

f_-a(x)=x³-3(-a)²x+2(-a)^3 = x^3 -3a^2 x - 2a^3 

---

Ja du hast Recht. ich denke die Aufgabe ist einfach nur falsch formuliert.

---

(Nicht Symmetrie)

Selbstverständlich liegt Symmetrie vor !

---

hj219: Zwischen f_a und f_-a. Wie denn genau?

---

der Graph von f_-a ist offensichtlich Nullpunkt-symmetrisch zum Graphen von f_a

---

Ok. Danke. Habe das unten ergänzt.

Answer 1

f_a(x)=x³-3a²x+2a³

Das entscheidende Wort in der Aufgabenstellung ist " berühren ".
Es soll nicht ein " Schnittpunkt " sondern ein " Berührungpunkt "
ermittelt werden.

f ´( x ) = 3*x^2 - 3*a^2
3*x^2 - 3*a^2 = 0
x^2 - a^2 = 0
x^2 = a^2
x = a
x = -a

f ( a ) = a^3 - 3*a^2*a + 2*a^3
f ( a ) = a^3 - 3*a^3 + 2*a^3 = 0
( a  | 0 )
Bei a = 0 ist die Steigung 0 und der Punkt
liegt auf der x-Achse. Berührpunkt.

f ( -a ) = (-a)^3 - 3*(-a)^2*a + 2*a^3
f ( a ) = -a^3 - 3*a^3 + 2*a^3 = - 2*a^3
( a  | -2*a^3 )
Dieser Punkt liegt nicht auf der x-Achse.

Symmetrie kommt vielleicht später.

mfg Georg

Comments

Meine Gedanken zu Symmetrie : siehe meinen Kommentar bei Lu

---

Die Frage zur Symmetrie ist die bisher tückischste die ich
kenne. Üblicherweise wird für 1 Funktion nach Symmetrie
gefragt. Meist Achsensymmetrisch zur y-Achse bzw.
Punktsymmetrisch zum Ursprung ( 0 | 0 ).
Das nach Symmetrie bezüglich 2 Funktionen kommt selten
vor.
f_-a ist aus Parallelverschiebung von f_a in Richtung y-Achse
entstanden. Ich habe mir beide Funktionen einmal zeichnen
lassen und konnte keine Symmetrie erkennen.
Diese ist aber doch vorhanden. Einen Beifall für Gast hj219. 

Es bliebe nur noch die Frage wie kann ich eine eventuell
vorhandene Symmetrie ( alle möglichen Symmetrien sind
ja denkbar ) mathematisch ermitteln ?

Ich versuche einmal

Achsensymmetrie
f_a ( - x ) = f_-a ( x )
(-x)³ - 3 * a² *(- x) + 2 * a³  =  x³ - 3 * a² * x - 2 * a³
stimmt nicht

Punktsymmetrie zu ( 0 | 0 )
- f_a ( - x) =  f_-a ( x )
- [ (-x)³ - 3 * a² *(- x) + 2 * a³  ] =  x³ - 3 * a² * x - 2 * a³
x³ - 3 * a² *x - 2 * a³  =  x³ - 3 * a² * x - 2 * a³
stimmt

Im Nachhinein war die Frage nach doch etwas einfacher
als gedacht.

---

Vielen Dank georgborn, Lu und hj 219 für eure schnelle Hilfe!

Dank euch hab ich das Ganze jetzt verstanden  :)

Das ist echt das beste Matheforum, dass ich kenne!

Besten Dank!

---

Gern geschehen. Die Frage war auch für mich lehrreich.

Answer 2

 f_a(x)=x³-3a²x+2a³

f_a'(x) = 3x^2 - 3a^2 = 3(x^2 -a^2) = 3(x-a)(x+a)

Extremalstellen x1= a und x2=-a unter der Annahme a≠0. Fall a=0 müsstest du noch separat untersuchen.

Nun kontrollieren, ob dort gerade eine Nullstelle liegt.

f_a(a) = a^3 - 3a^3 + 2a^3 = 0

Also f_a(x) berührt die x-Achse im Punkt A(a,0) für alle a ≠0.

f_a(-a) = -a^3 + 3a^3 + 2a^3 = 4a^3. Keine Berührung in der 2. Extremalstelle.

f_a(x) selbst ist symmetrisch zum Punkt P(0,2a^3)

Das ist der Wendepunkt der Parabel 3. Grades. Allerdings ist das selten gefragt.

Comments

f_a symmetrisch zu f_-a ist. 
f_a ( x ) = x³ - 3 * a² * x + 2 * a³
heißt doch
f_-a ( x ) = x³ - 3 * (-a)² * x + 2 * (-a)³
f_-a ( x ) = x³ - 3 * a² * x - 2 * a³

Mit symmetrisch ist meist die Symmetrie zur y-Achse gemeint.
Dürfte also nicht symmetrisch sein.

---

georgborn: Habe ich oben im Kommentar schon kritisiert. 

hj219 sieht das anders.

---

f_a(x)=x³-3a²x+2a³                          |Spiegelung an x-Achse

-f_a(x) =-(x^3 - 3a^2 x + 2a^3) = -x^3 + 3a^2 x - 2a^3 

f_-a(x)=x³-3(-a)²x+2(-a)³ = x³ -3a² x - 2a³             |Spiegelung an y-Achse

f_-a(-x) = -x^3 + 3a^2 x - 2a^3

Beide Spiegelungen zusammen: Spiegelung an P(0,0)

Nur: Warum habe ich dann gleichzeitig eine Parallelverschiebung um -4a^3 ?

Ok. Das geht, da der Wendepunkt ja auf der y-Achse liegt, bei + resp. - 2a^3

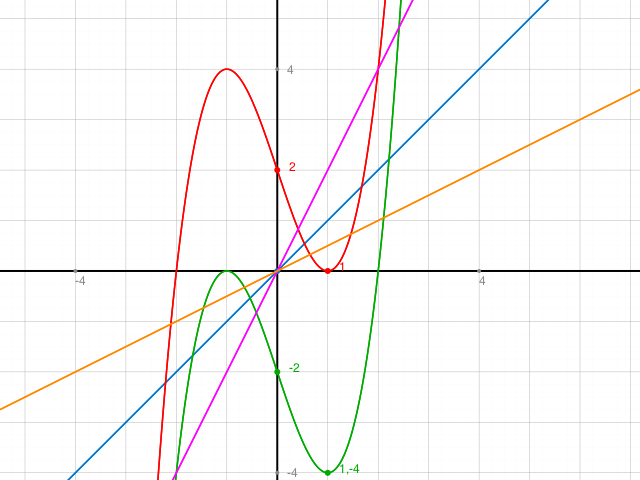
Hier noch ein Graph für a=1.

Man sieht, dass bei allen Geraden durch 0(0,0)  eine Spiegelung möglich ist.