P(2|5), Q(-1|8)
y = mx + b
m = (5-8)/(2+1) = -3/3 = -1
P eingesetzt
5 = -2 + b | b = 7
f(x) = -x + 7
Das hast Du korrekt berechnet!
Zur Überprüfung, ob R(-12|5) auf dem Graphen von f(x) liegt, setzt Du einfach seine x- bzw. y-Koordinate in die Funktionsgleichung ein; ist 5 = f(-12), dann liegt R auf dem Graphen, ansonsten nicht.
f(-12) = 12 + 7 = 19 ≠ 5
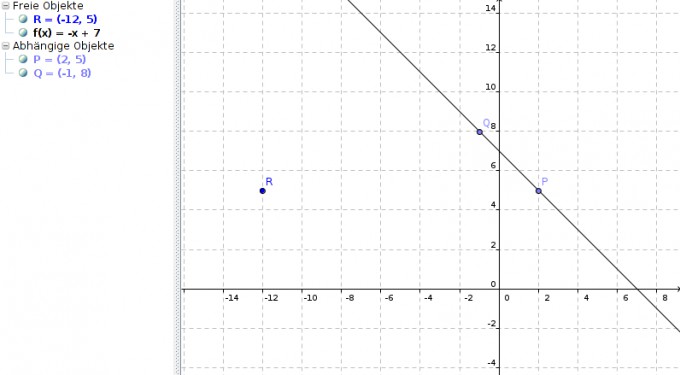
R liegt also nicht auf dem Graphen von f(x):
Besten Gruß