Aufgabe mit Brüchen per P-Q-Formel lösen: (3x^2-1)/2 - (4x^2+2)/3 - (2x^2-6)/4 = 0

Question

3x² - 1            4x² + 2          2x² - 6

---------   -      -----------  -   ------------    =  0

    2                     3                   4

 

die p-q formel bitte

Answer 1

Zuerst bringe ich die Gleichung auf die Form x^2+px+q=0:

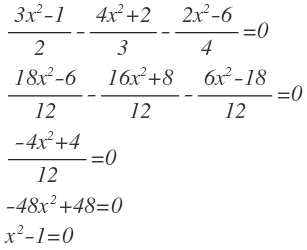
\frac { { 3x }^{ 2 }-1 }{ 2 } -\frac { { 4x }^{ 2 }+2 }{ 3 } -\frac { { 2x }^{ 2 }-6 }{ 4 } =0\\ \frac { { 18x }^{ 2 }-6 }{ 12 } -\frac { { 16x }^{ 2 }+8 }{ 12 } -\frac { { 6x }^{ 2 }-18 }{ 12 } =0\\ \frac { { -4x }^{ 2 }+4 }{ 12 } =0\\ -48{ x }^{ 2 }+48=0\\ { x }^{ 2 }-1=0

Nun kann ich p und q ablesen: p=0, q=-1

Einsetzen in pq-Formel:

x_1,2=±√(1)

x_1,2=±1

Comments

und wie komme ich auf die -4x² + 4    ?

                                                  -----------

                                                       12

---

Da die 3 Brüche nennergleich sind, kannst du die Zähler einfach subtrahieren: 18x^2-6-16x^2+8-6x^2-18=18x^2-16x^2-6x^2-6+8-18=-4x^2+4

---

Man kann eine Zeile davor , alles auf einen Bruchstrich setzten und zusammenfassen.

---

da kommt bei mir auf dem tachenrechner aber -20 raus :s, bei beiden aufgaben

---

jz kommt da 16 raus ?

---

x²(18-16-6) +18-6-8    probier mal diese Eingabe

---

jz kommt 20 raus :o

---

Vergiss den Taschenrechner, da hat man oft Probleme mit Klammern (vor allem bei Brüchen); und diese Aufgaben schafft man noch locker im Kopf.

18-16-6=2-6=-4 und -6-8+18=-14+18=4

Answer 2

am besten hier erst einmal auf den Hauptnenner bringen und zusammenfassen

 der HN =12

(6(3x²-1)-4(4x²+2)-3(2x²-6)) /12 =0

(18x²-6-16x²-8-6x²+18) /12=0         |Zusammenfassen

-4x² /12+4/12=0                 | * -12/4

x²-1=0         Fakorisieren, 3.binomische Form

(x-1)*(x+1) =0        x₁=1    x₂=-1