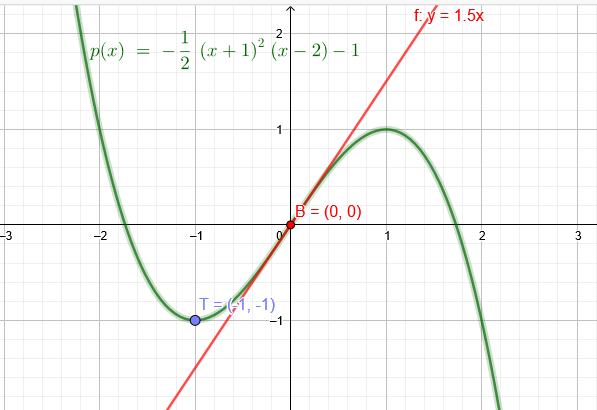
Ganzrationale Funktion 3. Grades hat den Tiefpunkt T(-1 | -1). Die Tangente an das Schaubild im Ursprung hat die Steigung \( \frac{3}{2} \) . Funktionsterm gesucht
Tiefpunkt T(-1 | -1) →Tiefpunkt T´(-1 | 0)
Ursprung (0|0) → P(0|1)
\(f(x)=a*(x+1)^2*(x-N)\)
\(f(0)=a*(0+1)^2*(0-N)=-a*N\)
\(-a*N=1→a=-\frac{1}{N}\)
\(f(x)=-\frac{1}{N}*[(x+1)^2*(x-N)]\)
\(f´(x)=-\frac{1}{N}*[(2x+2)*(x-N)+(x+1)^2]\)
\(f´(0)=-\frac{1}{N}*[2*(0-N)+(0+1)^2]\)
\(-\frac{1}{N}*[-2N+1]=\frac{3}{2}\)
\(N=2\) \(a=-\frac{1}{2}\)
\(f(x)=-\frac{1}{2}*(x+1)^2*(x-2)\)
\(p(x)=-\frac{1}{2}*(x+1)^2*(x-2)-1\)