Funktionen auf Nullstellen untersuchen

Question

Ich suche die Nullstellen, Extrema und Wendepunkte bei der Funktion f(x) = x³ - 3x² +3x

Außerdem ist die Skizze des Graphen gefragt.. -.-

Answer 1

Hi,

Nullstellen:

f(x) = x³ - 3x² +3x

x(x²-3x+3)

x_1,2,3=0 

Ableitungen:

f'(x)= 3x²-6x+3

f''(x)= 6x-6

f'''(x)= 6

Extrema:

f'(x₀)=0

3x²-6x+3=0 |:3, dann pq-Formel

x_1/2=1

f''(x₀)<0  Hochpunkt
f''(x₀)>0 Tiefpunkt

Es gibt es kein Extrema. Es gibt aber ein Sattelpunkt:

Schirrte um ein Sattelpunkt zu berechnen:

1. Wir leiten die Funktion f(x) dreimal ab.
2. Wir setzen die erste Ableitung Null
3. Wir setzen die zweite Ableitung Null
4. Sofern möglich, setzen wir diesen X-Wert in die dritte Ableitung ein
5. f'''(x) muss dann ungleich Null sein
6. Der X-Wert wird in f(x) eingesetzt, um den zugehörigen Y-Wert zu bestimmen

-> Sattelpunkt bei S(1|1)


Wendepunkt:

f''(x₀)=0

6x-6=0 |+6

6x=6 |:6

x=1

f'''(x₀)≠0
f'''(1)≠0

Wendepunkt bei W(1|1)


Skizze:





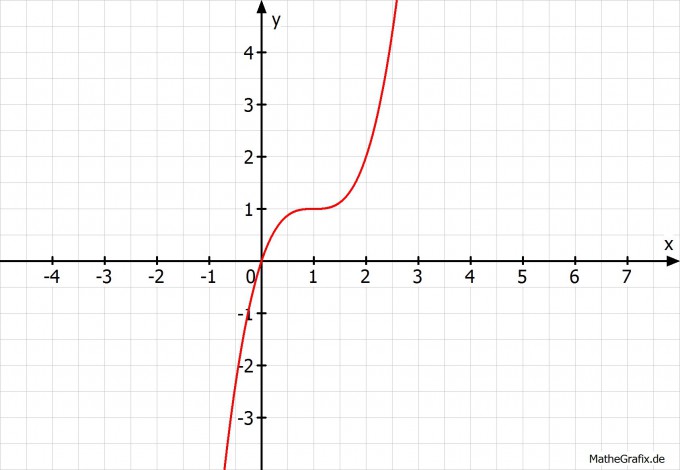
Alles klar?