Wie finde ich das Minimum von x + y?

Question

Wenn x und y positive, reelle Zahlen sind und es gilt xy=1, wie kann ich dann das Minimum für x+y bestimmen?

Answer 1

Es gilt

x * y = 1
y = 1/x

Und es soll folgende Funktion minimal werden:

f(x,y) = x + y

Ich ersetze das y mit der Nebenbedingung

f(x) = x + (1/x)

Wenn das Minimal werden soll muss die Ableitung 0 werden:

f '(x) = 1 - 1/x^2 = 0
x^2 - 1 = 0
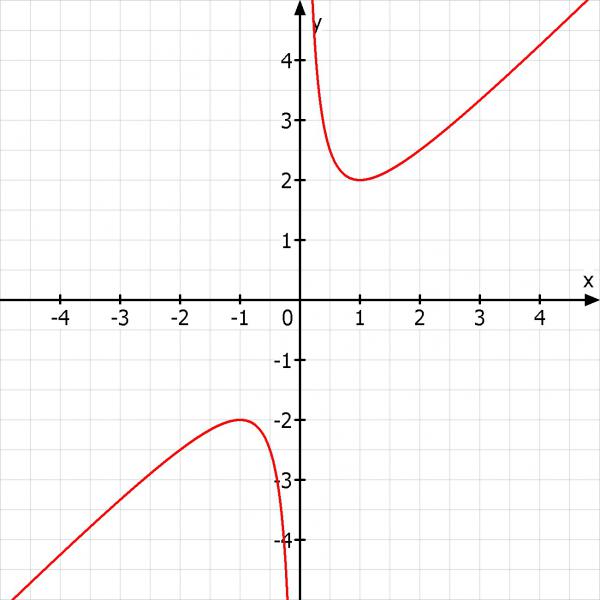
x = 1 und x = -1 (nicht im Definitionsbereich)

Wenn wir also mal x mit 1 annehmen, wäre y auch 1 und x + y wäre 2. Das ist dann das Minimum.

Skizze: